Biophysics Problem 31
When standing erect, a person's weight is supported chiefly by the larger of the two leg bones. Assuming this bone to be a hollow circular tube of \(2.5 \;cm\) internal diameter and \(3.5 \;cm\) external diameter, what compressive load must this bone (in each leg) carry in the case of a \(70 \;kg\) person?
First of all, you must make a diagram of the cross-section of the bone. Draw a diagram on a piece of paper.
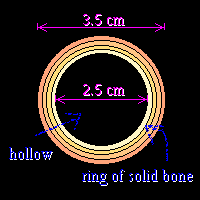
Remember that the \(70\;kg\) represents the person's mass, and thus is not a force.
Calculate the downward force.
You should have had
\(\text{downward force} = 70 \;kg \times 9.8\; m/s^2 = 686\; N\)
Now calculate the cross-sectional area of the bone.
Remember that the area of a circle is: \(A = \pi r^2\)
Cross-sectional area, we'll call \('A' \)is:
\(A = \pi (3.5/2)^2 - \pi (2.5/2)^2 \\ = 9.62 - 4.91 \\ = 4.71\; cm^2 \\ = 4.71 \times 10^{-4}\; m^2\)
Now calculate the compressive load -- that is, the force per unit area of bone. Remember that there are two bones, each carrying an equal share of the load.
Compressive load, we'll call \('CL'\) is:
\(CL = \frac{force}{unit\;area\;of\; bone} \\ = \frac{686\; N}{2 \times 4.71 \times 1-^{-4}} \\ = 7.3 \times 10^5 \; Nm^2\)