Problem 4-23 - Projectile - Part 10 - A
A girl throws a ball onto the roof of a house, as illustrated in the figure, and prepares to catch the ball with a baseball glove held \(1.0\; m\) above the ground. The ball rolls off the roof with a speed of \(3.2\; m/s.\)
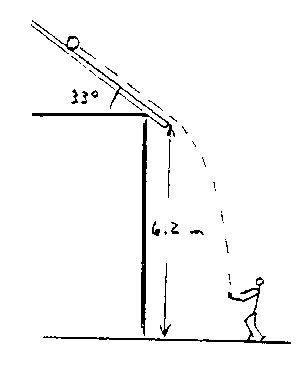
(a) From the time the ball left the roof, how long will it take to land in her glove?
(b) How far from the horizontal edge of the roof should she hold her glove?
(c) What is the ball's velocity as it reaches her glove?
Accumulated Solution

\(v_{0_x} = v_0\cos33 = 2.68\; m/s \\ v_{0_y} = v_0\sin33 = 1.74\; m/s \\ y = v_0{_y{^t}} + (1/2)a_yt^2\\ 4.9\;t^2 + 1.74\;t - 5.2 = 0 \\ t = 0.868\; s \\ x = 2.3\;m \\ v_y = 10.25\; m/s\\ v = [(12.68)^2 + (10.25)^2]^{1/2} = 10.6\; m/s\)
Correct

\(\theta\) is given by:
\(\theta = \tan^{-1} |v_y|/|v_x| = \tan^{-1}(10.25)/(2.68) = 75^\circ\)
The ball's velocity is \(10.6\; m/s\) at \(75^\circ\) below the horizontal (ans. to (c))
You have completed this problem.