Biophysics Problem 11
A horse pulls an old-fashioned cutter along a level icy surface at a steady speed of \(15\; m/ s.\) The cutter and its load have a total mass of \(250\; kg.\) If the horse is providing a constant pulling force of \(125\; \text{newtons,}\) what is the coefficient of friction?
First make a diagram showing all the forces acting on the cutter.
Your diagram should look similar to the one below.
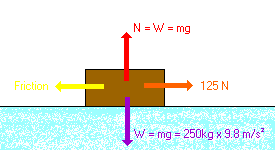
Think about this question:
What is the magnitude of the acceleration of the cutter?
The cutter is moving at constant velocity. Therefore, the \(\text{acceleration} = 0.\)
Now think about this question:
What is the magnitude of the sum of the horizontal forces?
Since the \(\text{acceleration} = 0,\) the system is in translational equilibrium. Therefore, the sum of the forces in any direction must equal zero.
It follows that the sum of forces in the horizontal must also equal zero.
Another question:
Since the horizontal forces must sum to zero, what is the magnitude of the frictional force?
There are only 2 horizontal forces, and they must sum to zero.
It follows that the frictional force must be \(125 \;N.\)
Now all that you need is the formula relating friction and the normal force.
\(F_{Friction} = \text{coefficient of friction}\; \times \text{Normal Force}\)
Try to calculate the coefficient of friction.
Your calculations should have been as follows:
\(F_{Friction} = \text{coefficient of friction} \times \text{Normal Force} \\ \text{coefficient of friction} = \frac{F_{Friction}}{Normal\; Force} \\ = \frac{125\; N}{250\; kg \times g}\\ = 0.051\)
Remember, the answer is a dimensionless ratio.