Biophysics Problem 14

You are walking along a wood floor. During the walking process your heel strikes the floor with a force \(F\) at an angle  \(\theta\)  to the vertical. If  \(\mu_s= 0.5\) for the normal shoe leather on wood, what is the maximum value that \(\theta \) can take and still ensure that you do not slip?

First make a diagram.

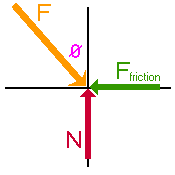
diagram illustrating the forces of walking on a floor and striking your heel

If you don't slip, you must be in translational equilibrium.

All horizontal forces must add up to zero.
All vertical forces must add up to zero.

Before you can do this you must replace F with its horizontal and vertical components.

Now we know that the force of friction is:

\(\text{Force Friction} = 0.5 \times \text{Normal Force}\)

so we will make this substitution into our diagram.

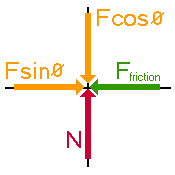
diagram illustrating forces and friction of heel striking floor

Now we are ready to balance all the horizontal forces to get one equation, and balance all the vertical forces to get the second equation.

Once we do this, we can solve the two equations simultaneously to find \(\theta.\)

Write down the two equations relating to translational equilibrium.

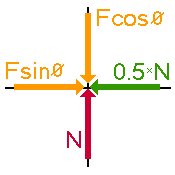
diagram indicating all forces of strking heel on the floor

The equations are:

\(F\; \sin \theta = 0.5 \; N \\ F\; \cos \theta = N\)

 Now try to solve these equations to find \(\theta.\)

\(F \sin \theta = 0.5 \; N \\ F \cos \theta = N\\ \frac{\sin \theta}{\cos \theta}=0.5\\ \tan \theta = 0.5 \\ \theta = 26.6^\circ\)

The first equation is divided by the second, causing the \('F'\) and \('N'\) to cancel out.

Therefore, the maximum value is  \(\theta = 26.6^\circ.\)