Biophysics Problem 2
A butterfly is flying in a garden. First it travels due south for \(6.0 \;m\) and then \(37 \;W\) of \(N\) for \(10 \;m.\) Assuming that the positive \(x\)-direction is east, and the positive \(y\)-direction is north,
(a) what are the coordinates of the butterfly's final position relative to its initial position?
(b) what are the magnitude and direction of the displacement of the butterfly (relative to its initial position)?
Start by making a diagram, approximately to scale, showing the butterfly's path. Mark on this the vector required in (b).
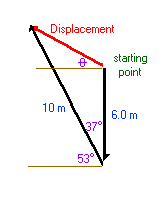
Calculate the north and west components of the second portion of the flight.
Combine these with the displacement during the first part to find the final coordinates of the flight.
Finally, use the initial coordinates (0,0) and the final to find the net displacement and the angle \(\theta\).
For the second portion of the flight, the westerly displacement will be:
\(\mathrm{10.0\;m \times \cos(53^\circ ) = -6.0\;m}\)
And the northerly component will be:
\(\mathrm{10.0\;m \times \sin(53^\circ ) = 8.0\;m}\)
Therefore the net north-south displacement will be:
\(\mathrm{-6.0\;m + 8.0\;m = + 2.0\;m}\) (ie: It will be \(\mathrm{2\;m}\) north of its initial positon.)
And the east-west displacement will be: \(\mathrm{-6.0\;m}\)
So the final coordinates (in m) will be: \(\mathrm{(-6.0, 2.0)}\)
The displacement from the starting point (0,0) will be:
\(\mathrm{displacement = \sqrt {(6.0^2 + 2.0^2)} \\ = 6.3\; m}\)
\(\mathrm{And \tan (\theta) = 2/6 \\ = 0.333 \\ therefore\; \theta = 18^\circ \; north \; of \; west}\)