Biophysics Problem 23
A \(100 \;kg\) man stands \(1\;m\) from the end of a \(4\; m\) scaffold which weights \(750\; N.\) What are the tensions \(T_1\) and \(T_2\) in the supporting ropes?
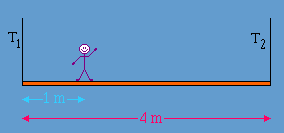
First redraw the diagram to show both vertical downward forces.
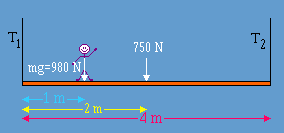
There are no horizontal forces. For translational equilibrium we only have to consider vertical forces. From this, you should be able to get:
\(T_1 + T_2 = 980\;N + 750\;N\)
But this is not immediately useful because there are two unknowns. The only way to proceed is to use the concept of rotational equilibrium. Set up an equation for the sum of the moments about \(A.\)
From rotational equilibrium, you should get
\(T_2 \times 4\;m = (980\;N \times 1\;m) + (750\;N \times 2\;m\)
Solve the above equation for \(T_2,\) and then use the first equation to get \(T_1.\)
The answers are:
\(T_1 = 1110\; N \\ T_2 = 620\; N\)