Biophysics Problem 26
Suppose the arm in Question 25 is thrust forward until the upper arm makes an angle of \(30^\circ\) from the vertical. The forearm stays level. Determine the new value for the quantities sought in Question 25.
You should not be attempting this question unless you've successfully completed Question 25.
It is important to realize that when the arm is thrust forward, \(F_m\) will remain parallel to the upper arm bone. Therefore \(F_m\) will also be at \(30^\circ \) from the vertical.
While the upper arm bone is at \(30^\circ\) from the vertical, the force exerted by it will not necessarily be parallel to the bone.
Draw a diagram of this problem.
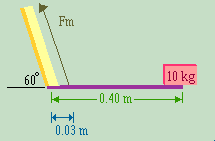
Your diagram should look something like the one above.
Note that \(F_m\) has both a vertical component (upward) and a horizontal component (towards the left). The upper arm must exert both a vertical downward force and a horizontal force to the right.
Further, the horizontal component of \(F_m\) and of the upper arm bone must be equal and opposite since they are the only two horizontal forces.
You should also realize that the lines of action of these two horizontals will both pass through the point where the two bones make contact.
Therefore, if you take moments about this point, you will have an equation involving only the force of gravity on the mass, and the vertical component of the muscle force.
Set up this equation and solve for the vertical component.
As in the previous problem, the force of gravity on the mass in the hand will be:
\(W = m \;g \\ W = (10\; kg) (9.8\; m/s^s) \\ W = 98 \;N\)
Let's call the point where the two bones make contact \('A'\) and the vertical component of \(F_m\) as \(F_m(v).\)
The equation then becomes
\( \sum M \;(\text{about}\; 'A') = (F_m(v) \times 0.03 \;m) - (98\; N \times 0.40\; m) = 0\)
Solving this gives \(F_m(v) = 1307\; N.\)
Now let's look at the vertical components.
There are three vertical components which must add up to \(0.\) These are gravity \((m\;g),\) and \(F_m(v),\) both of which we already know, and \(F_b(v)\) (the vertical component of the force exerted by the bone.
Set up an equation for this, and solve for \(F_b(v).\)
Your equation should look like this
\(\sum F(v) = F_b(v) + F_m(v) + m \;g \\ 0 = F_b + 1307\; N - 98\;N \\ F_b = -1209\; N\)
i.e. \(F_b\) acts downward.
We now have all vertical forces, but still have to find the equal and opposite horizontal components of \(F_b\) and \(F_m.\)
Draw another diagram to show all horziontal and vertical forces.
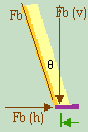
The next step will be to use \(F_m(v)\) to calculate \(F_m\) and \(F_m(h).\) Once you have \(F_m(h),\) you should know what \(F_b(h)\) is.
Since \(F_m\) is \(30^\circ\) from the vertical, then
\(\cos 30^\circ = F_m(v) / F_m \\ F_m = F_m(v) / \cos 30^\circ = 1510\; N \\ F_m(h) = F_m \sin 30^\circ = 755 \;N\)
This is the magnitude of \(F_m(h).\) It obviously acts to the left, and should therefore be stated as \(F_m(h) = -755 \;N.\)
\(\sum F(h) = F_b(h) + F_m(h) = 0\)
Therefore \(F_b - 755 \;N = 0\)
And we find that \(F_b(h) = 755\;N\)
We have all we need to calculate \(F_b\) and the direction it makes with the vertical. Remember the force exerted by the bone does not have to be parallel to the bone.
Your calculations should look like this:
\(\tan \theta = \frac{F_b(h)}{F_b(v)}\\ = 0.624 \\ \theta = 32^\circ \; \text{from the vertical}\)
\(F_b = \sqrt{F_b(v)^2 + F_b(h)^2}\\ F_b = 1425\;N\)