Biophysics Problem 27
A \(10 \;N\) force at an angle of \(35^\circ\) to the horizontal is applied to the \(5\; kg\) block. In addition there is a \(7 \;N\) frictional force acting as shown.
(a) Find the work done by each of the four forces acting on the block in moving it \(12 \;m\) horizontally.
(b) What is the total work done?
(c) If the block starts from rest, what is the speed after moving the \(12\;m\)?
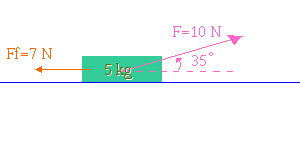
The diagram shows two forces acting on the block. The question implies that there are two other forces. Can you identify them?
Add the extra two forces to your diagram.

You should be able to tell immediately the work done by the last two forces you added.
What is the force of gravity?
A force (or a component of a force) that is perpendicular to the displacement does no work. Since the displacement is horizontal, and the gravity force vector is vertical, there is no work done by this force.
Similarly, there is no work done by the normal force.
Calculate the work done by the \(10 \;N\) force. Remember that only its horizontal component can do any work.
A force (or a component of a force) that is perpendicular to the displacement does no work. Since the displacement is horizontal, and the gravity force vector is vertical, there is no work done by this force.
Similarly, there is no work done by the normal force.
Calculate the work done by the \(10\; N\) force. Remember that only its horizontal component can do any work.
The work done by the horizontal component of the \(\mathrm{10\; N}\) force will be
\(\text{work} = \text{horizontal component} \times \text{displacement} \\ W = (10\; N \cos\;35^\circ) \times 12 \;m \\ W = 98.3 \;J\)
Now find the work done by the frictional force, \('Ff'.\) The force and displacement are in opposite directions, so the work done is negative.
The work done by the frictional force is:
\(W = \text{force} \times \text{displacement} \\ W = 7 \;N \times -12\; m \\ W = -84\; J\)
You are done with part (a).
Total work done is the algebraic sum of the work done by each of the components. So the total work done is
\(W_{total} = W_{10\;N\; force} + W_{friction} + W_{gravity} + W_{normal} \\ W_{total} = 98.3 - 84 + 0 + 0 \\ W_{total} = 14.3\; J\)
You are done part (b) now.
The total work done on the block will equal the change of mechanical energy of the block. There is no change in the potential energy of the block, so only the kinetic energy will change.
Therefore: \(\text{total work done} = \text{change in kinetic energy}\)
Calculate the value of the speed.
Remember that \(\text{total work done} = \text{change in kinetic energy.}\) From part (b), we found that the total work done is \(14.3 \;J.\) Since the block starts from rest, the change in kinetic energy will be the final kinetic energy, \((m\; v^2)/2.\) The mass was given in the question \((m = 5\; kg).\) So we get
\(14.3\;J = (m \;v^2) / 2 \\ v = 2.4 \;m/s\)