Biophysics Problem 41
In a circus act, a pony and a horse are balanced on a teeter-totter. If the pony is 12 hands high and the horse is 18, then what will be the ratio of the distances?
\(\mathrm{\frac{Pony\;to\; pivot\;point}{Horse\; to\; pivot\; point}(approximately)?}\)
This problem involves both scaling and rotational equilibrium. Don't worry that the unit 'hand' has not been defined. Since you will be working with ratios, the actual size of a 'hand' is not required.
Start by making a simple diagram of the system.
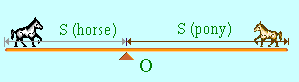
We must determine the scaling factor (which we'll call \('L'\)), before we can procede any further.
The linear dimensions for the horse are greater than those of the pony by a factor \('L'\). The height of the horse (18 hands) is 1.5 times greater than that of the pony (12 hands). So \(L = 1.5.\)
Now what is the ratio of the mass of the horse to that of the pony?
Remember that the ratio of the masses will be the same as the ratio of the volumes.
Since volume scales as \(L^3,\) the ratio is \((1.5)^3 = 3.375.\)
I hope you realize that the ratio of the weights will be the same as the ratio of the masses. (Think of \(W = m\; g.\))
Now we are ready to consider the rotational equilibrium of the system. Of course, it is preferable to take the moments about the pivot point \('O'\) (rather than taking the moments about one end of the teeter-totter).
Set up your equation for rotational equilibrium about \('O',\) and solve your equation for the ratio \(\mathrm{S_{pony} / S_{horse}}\)
Remember, in rotational equilibrium, the sum of the moments is zero. There is a counter-clockwise (positive) moment due to the horse, and a clockwise (negative) moment due to the pony. So your equation should be:
\(\mathrm{W_{horse} S_{horse} - W_{pony} S_{pony} = 0}\)
From this, you should be able to get:
\(\mathrm{S_{pony} / S_{horse} = W_{horse} / S_{pony} = 3.375}\)