Biophysics Problem 5

A bird is flying due north with a speed of \(15 \;m/s.\) A train is travelling due east with a speed of \(15\; m/s.\) What are the magnitude and direction of the velocity of the bird from the point of view of a passenger in a train?

To determine the velocity of the bird relative to a person on the train, we must put ourselves in the frame of reference of the person on the train. To do this, we'll do two quick experiments.

We'll start with the bird remaining stationary. Imagine that you are somewhere on the train, looking at the bird.

diagram of bird flying above train.


From your frame of reference on the train, in which direction did the bird appear to move?

diagram of bird flying above a train moving to the right

From your frame of reference, the bird appeared to move in a westerly direction at 15 m/s.

 Let's allow the bird to fly now to see the other component of its motion.

Now both object are about to move. Again, imagine that you are somewhere on the train, looking at the bird.

The new component is simply the bird's northerly flight at \(15 \;m/s.\)
bird flying north away from train travelling west

Now that we have the magnitude and direction of the two components of the bird's movement relative to a person on the train, all that we need to do is make a velocity vector triangle to calculate the net velocity of the bird. Do this on a piece of paper.
 

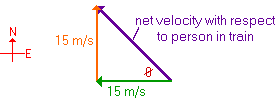
diagram of triangle indicating path and direction of bird, path and direction of train

\(\mathrm{net\; velocity = \sqrt{15^2 + 15^2 \;m/s}\\ 21.2\;m/s\\ \tan \theta = \frac{15\; m/s}{15\;m/s} = 1.0 \\ \theta = 45^\circ}\)

In terms of compass directions, the bird's velocity with respect to a person on the train is \(\mathrm{21.2 \;m/s}\) to the northwest.