Biophysics Problem 6

A bird is migrating non-stop a distance of \(\mathrm{2000\; km.}\) Its destination is due south of its present position. In still air, the bird can fly with a speed of \(\mathrm{40\; km \;hr.}\)However, there is a wind of \(\mathrm{25\; km \;hr}\) from the west.

(a) In order to make the trip following a straight line path, in what direction should the bird head?
(b) How long will the trip take?

In this problem, we are dealing with motion in 2 different frames of reference:

  • motion with respect to the wind and
  • motion with respect to the land.

 To illustrate this, we'll do a little experiment.

Pretend that the bird is supended in the air like a balloon, with the wind blowing towards the east at \(\mathrm{25\; km/hr.}\)

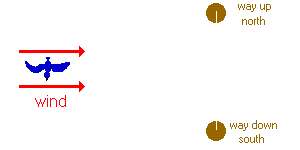
diagram indicating wind directions around a flying bird

Noticed that the bird did not move with respect to the wind.

 It did move with respect to the ground.

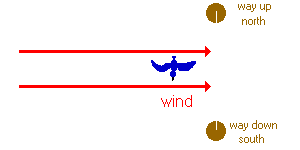
diagram of bird flying in the wind

Let's do the experiment again, this time letting the bird move in a westerly direction at \(25\; km/hr \)with respect to the wind. (the wind is still blowing at \(25\; km/hr \) to the east).

Notice that this time, the bird's westerly motion is counteracted exactly by the easterly motion of the wind, so that the bird did not move with respect to the ground.

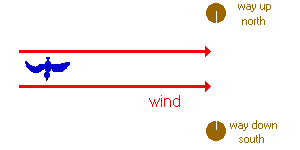
bird flying in the wind

 

Our goal is to point the bird in such a direction so that it heads due south with respect to the ground; That is, so that it has no east-west motion with respect to the ground. Let's review what we know already:

  1. The bird can fly at \(40\; km/hr \) with respect to the wind.
  2. In order for the bird to have no east-west motion wrt the ground, it must fly at \(25\; km/hr \) to the west wrt the wind.

Thus, in order for the bird to have a net velocity due south with respect to the ground, roughly in what direction should it fly?

In order to have a net velocity due south with respect to the ground, the bird must fly to the south-west in such a drection that its east-west component of motion is \(25\; km/hr\) to the west.

The angle can be determined by constructing a velocity vector diagram.

 

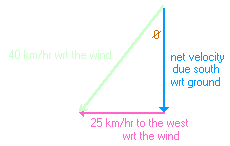
diagram indicating velocity

\(\mathrm{velocity \; due \; south = \sqrt {40^2 - 25^2 km/hr} \\ 31.2\; km/hr\\ \sin \theta = 25/40 = 0.625\\ \theta = 38.7^\circ}\)

Therefore, the answer to part (a) is that the bird must fly in a direction \(\mathrm{38.7^\circ}\) west of south.

 To solve part (b), we simply need to divide the length of the bird's trip by the due south component of its velocity:

\(\mathrm{ time = 2000\; km / 31.2\; km/hr \\                  = 64.1 \;hr}\)