Biophysics Problem 7

A boat is going to head due north, but unfortunately the tide is running out (east) with a speed of \(11 \;m /s.\) If the boat can travel with a maximum speed of \(15 \;m /s\) in still water, what is the maximum speed with which it can head due north relative to the shore?

In this problem, we are dealing with motion in 2 different frames of reference:

  • motion with respect to the water, and
  • motion with respect to the shore.

We will illustrate this with a little experiment.

Let's simulate the out-going tide.

Note the motion of the boat (which is just floating on the water) with respect to the shore and with respect to the water.

diagram of boat and shore

 Notice that while the boat did not move with respect to the water as the tide went out, it did move with respect to the shore.

diagram of boat in water as tide goes out

Let's try the experiment again, this time with the boat travelling westward (towards the shore) at \(11 \;m/s\) with respect to the water.

Notice that the boat moved with respect to the water, but did not with respect to the shore because it's westward motion counteracted exactly the motion of the out-going tide.

We want the boat to travel due north with respect to the shore, that is, without any east-west motion with respect to the shore.

 Let's review what we already know:

  1. the maximum speed of the boat is \(15\; m/s\) with respect to the water.
  2. in order to have no motion wrt the shore, the boat must have a velocity of \(11\; m/s\) to the west wrt the water.

Thus, in order to have a maximum net velocity due north wrt the shore, the boat must move at \(15 \;m/s\) (wrt the water) in a direction towards the north-west such that its east-west component is \(11\; m/s\) to the west.

Make a diagram of the velocity vector triangle.

Here is the diagram and calculation. 

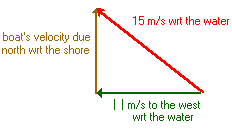
diagram of a boat

\(\text{velocity due north} = \sqrt {15^2 - 11^2\;m/s }\\=10.2\;m/s\)