Biophysics Problem 9
The mass in the diagram slides along a horizontal frictionless floor, pulled by the force \(F\) as shown. What is the acceleration?
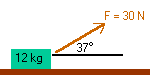
You should be able to find the net force in the horizontal direction and then substitute into Newton's second law \((F=ma)\) to find the acceleration.
Since there is no friction, the only horizontal force is the horizontal (or \('x'\)) component of the \(30\;N\) force.
Remember, the force \(F\) made an angle of \(37^\circ\) with the horizontal.
Also, the magnitude of \(F\) is \(30\;N.\)
The horizontal component could be represented by \(F_x\) or \(F_H\)
\(\text{Since}\; \cos 37^\circ = F_H/F \\ F_H = F \times \cos 37^\circ \\ = (30\; N) \times 0.8 \\ = 24\; N\)
Now calculate, using Newton's second law, the magnitude of the acceleration.
Newton's second law is \(F = ma.\)
Where \(F\) is understood to be the net force in the direction of the acceleration. In this case, there is only one force, in the right direction, and that is the force \(F_H = 24 \;N.\)
\(\text{Therefore,} \; F = m\times a \\ 24\; N = (12\; kg) \times a \\ a = 2 \; m/s^2 \; \text{to the right}\)