Electricity I

  1. If a current of \(3\; A\) is divided by the following circuit, the current flowing through the \(4\; \text{Ohm}\) resistor is … 

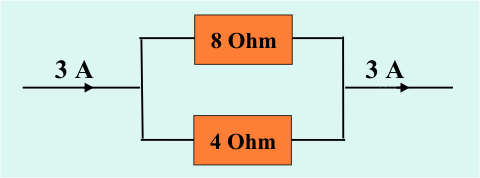
    Diagram of a circuit with two resistors
    (A)  3 A 
    (B)  2 A 
    (C)  1,5 A 
    (D)  1 A 

    Correct = B 
    The electric current splits up according to the resistance (low resistance high current and high resistance low current). If \(3\; A\) flow into the parallel connection \(2/3\) of \(I (2/3\; \text{of}\; 3A = 2A)\) will pass through the \(4\; \Omega \) resistor and \(1/3\) of \(I (1/3\; \text{of} \; 3A = 1A)\) through the \(8\; \Omega \) resistor.


     
  2. The diagram below shows part of a circuit into which a current \(I\) is flowing. Which ammeter shows the highest reading? 

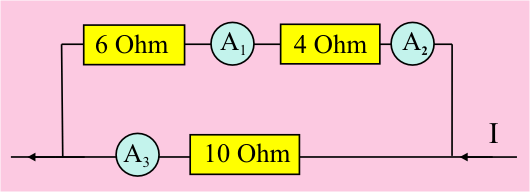
    Diagram of circuit with three resistors
    (A)  \(A_1\) 
    (B)  \(A_2\) 
    (C)  \(A_3\) 
    (D)  All three ammeters give the same reading 

    Correct = D 
    Since the total resistance is the same \((2\; \Omega + 8\; \Omega = 10\; \Omega)\) in both parts of the parallel connection all ammeters will show the same reading.


     
  3. The diagram below represents a part of a circuit containing an ohmic resistor, a voltmeter and an ammeter. If the reading on the ammeter \(A\) increases the reading on voltmeter \(V\) … 

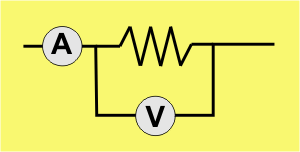
    Diagram of a circuit with a resistor

    (A)  increases in the same ratio. 
    (B)  increases, but not in the same ratio. 
    (C)  remains unchanged. 
    (D)  decreases in the same ratio.  

    Correct = A 
    Ohm´s Law: the current flowing through a conductor is directly proportional to the potential difference across it provided the temperature of the conductor remains constant. Or in formulae form: \(R = I/V,\) to keep \(R\) constant \(I\) and \(V\) have to increase/decrease at the same ratio.

     
  4.  A battery is connected to two identical light bulbs in parallel as well as another identical bulb in series. An ammeter and a voltmeter are also connected as shown in the circuit diagram below. 

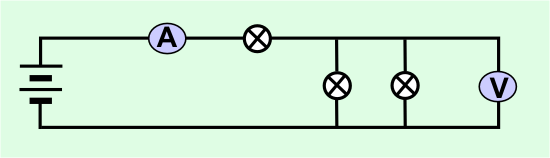
    diagram of a circuit with two lights in parallel and one in series

    One of the light bulbs connected in parallel is unscrewed. How will the ammeter and the voltmeter readings change? 
     
    Answer Voltmeter Reading Ammeter Reading
    (A) increases increases
    (B) increases decreases
    (C) increases unchanged
    (D) decreases decreases
     

    Correct = B 
    Unscrewing one of the parallel bulbs will change the total resistance of the circuit in a way that it goes up. Higher resistance will cause a lower current to flow through the circuit (option B and D). How is the p.d. affected? Prior to unscrewing the voltmeter measured the p.d. across one of the bulbs connected in parallel, which had a lower resistance since they were in parallel \((1/R_{total} = 1/R1 + 1/R2).\) After unscrewing a higher voltage is required to drive the current through the bulb » voltmeter reading goes up.


     
  5. A learner connects a circuit as shown in the diagram below. They use a source of electricity with an electromotive force (emf) of \(12\; V.\) 

    Which one of the following best gives the ammeter and voltmeter readings which the learner is most likely to get with this circuit? 
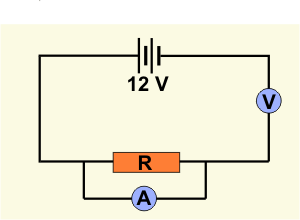
    Diagram of circuit with a voltmeter and resistor
     
    Answer Ammeter reading Voltmeter reading
    (A) reads zero reads zero
    (B) reads zero reads \(12\; V\)
    (C) very large reading reads zero
    (D) very large reading reads \(12\; V\)
     

    Correct = B 
    No current will flow in the circuit due to the position of the voltmeter. Voltmeters have a very high resistance - ammeters on the other hand have a very low resistance - and hence we can say that the resistance of the voltmeter blocks somehow the current. Since the voltmeter is connected across the terminals of the source of electricity it will measure the emf of the battery.


     
  6. Three identical resistors of \(4\; \Omega\) are connected to give a combined resistance of \(6\; \Omega\). Which of the following circuit diagrams illustrates how this was done? 

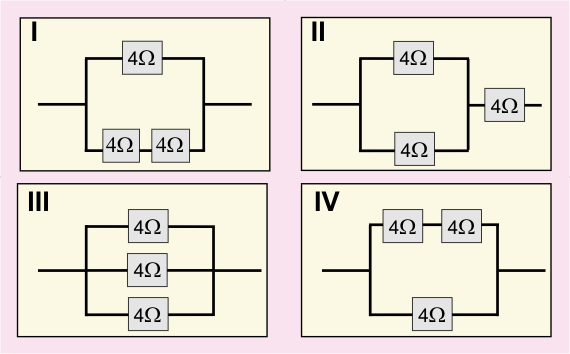
    Diagram with four images of different circuits in various configurations

    (A)  I 
    (B)  II 
    (C)  III 
    (D)  IV 

    Correct = B 
    Only in option B the effective resistance is \(6\; \Omega: 4\; \Omega\) and \(4\; \Omega\) in parallel - \(1/R = 1/4 + 1/4 = 1/2\) hence \(R = 2\; \Omega.\) \(4\; \Omega\) is in series with \(2\;\Omega\) hence \(R\; \text{combined} = 2\; \Omega + 4\; \Omega = 6\; \Omega.\)


     
  7. In the circuit below \(B_1, \;B_2\) and \(B_3\) are identical light bulbs. The internal resistance of the battery can be ignored. 
    Which statement is true regarding the relative brightness of the bulbs? 

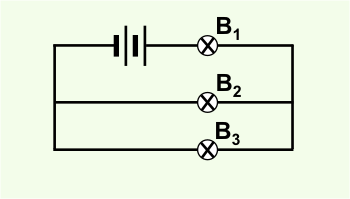
    Diagram of circuit with 3 resistors

    (A)  The three bulbs glow with the same brightness. 
    (B)  \(B_2\) and \(B_3\) glow with the same brightness but brighter than \(B_1.\) 
    (C)  \(B_2\) and \(B_3\) glow with the same brightness but less brightly than \(B_1.\) 
    (D)  \(B_1\) glows brighter than \(B_2\) while \(B_2\) in turn glows brighter than \(B_3.\)  

    Correct = C 
    \(B_2\) and \(B_3\) are connected in parallel, hence only \(50\%\) of the current will flow through each of those bulbs and the p.d. across them will be less than the p.d. across \(B_1\) (\(1/3\) of total p.d. will be across \(B_2\) and \(B_3;\) \(2/3\) of total p.d. across \(B_1\)). As a result \(B_1\) will shine brightest (power = current x voltage) and \(B_2\) and \(B_3\) will have the same brightness.


     
  8. Two identical light bulbs, \(X \) and \(Y,\) are connected in series as shown in the sketch below. 
    How will the brightness of the bulbs change if switch \(S\) is closed? 

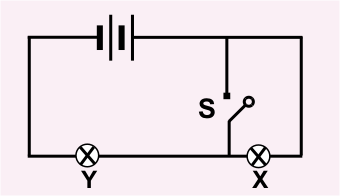
    diagram of a circuit with a switch
    Answer X Y
    (A) brighter brighter
    (B) dimmer dimmer
    (C) brighter not lit up
    (D) not lit up brighter
     

    Correct = D 
    After closing the switch no current will flow through \(X,\) hence it will not lit up (option D) and consequently a hgher current will pass through bulb \(Y\) making it shine brighter.


     
  9. A student connects three identical resistors as shown in the sketch below. 
    The potential difference across the battery is 12 Volt. What are the readings on \(V_1\) and \(V_2\) respectively? 

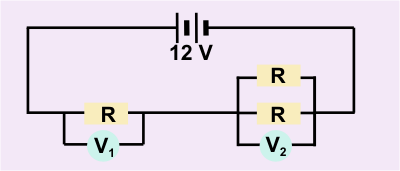
    diagram of circuit with 3 resistors and 2 voltmeters.
     
    Answer \(V_1\) \(V_2\)
    (A) 4 8
    (B) 6 6
    (C) 8 4
    (D) 9 3
     

    Correct = C 
    Correct answer is option C (see also question 6 & 7): \(2/3\) of total p.d. will be across single resistor \(R\) and \(1/3\) of total p.d. will be measured across resistors \(R\) in parallel by \(V_2 \cdot2/3 \cdot 12\;V = 8\;V; \) and  \(1/3 \cdot 12\;V = 4\;V\) across \(R\) in parallel.


     
  10. A \(9\; V\) battery is composed of six \(1,5\; V\) cells, which are connected in series. Each cell has an internal resistance of \(0,2\; \Omega.\) What is the highest current that can be obtained from such a battery? 

    (A)  7,5 A 
    (B)  1,5 A 
    (C)  1,2 A 
    (D)  0,3 A 

    Correct = A
    \(\text{Total internal resistance} = 6 \cdot 0,2\; \Omega = 1,2\; \Omega\)
    \(\text{Voltage} = 9\;V \\ I = V/R = 9/1,2 = 7,5\;A.\)