Energy, Work & Power 1

  1. An object moving in a straight line with a constant velocity has kinetic energy E and momentum p. If the speed of the object is doubled, the new value of kinetic energy and momentum will be … 
     
    Answer Kinetic Energy Momentum
    (A) \(2\; E\) \(2\; p\)
    (B) \(2\; E\) \(4\; p\)
    (C) \(4\; E\) \(p \)
    (D) \(4\; E\) \(2\; p\)
     

    Correct = D 
    \(E_k = 1/2\;mv^2,\) doubling \(v\) increases \(E_k\) by 4. \(p = mv,\) doubling \(v\) doubles the momentum. Only option D offers \(4\; E_k\) and \(2\; p.\)

     
  2. A ball is projected vertically upwards and then returns to the ground. Ignore all frictional forces. Which one of the following statements about the kinetic energy and potential energy of the ball is true? 

    (A) The kinetic energy is always equal to the potential energy. 
    (B) The kinetic energy is always less than the potential energy. 
    (C) The kinetic energy is always more than the potential energy. 
    (D) The sum of the kinetic energy and potential energy is always constant. 

    Correct = D
    Application of law of conservation of energy: energy cannot be created or destroyed, but can be changed from one form to another. On rising the potential energy increases as the kinetic energy decreases and on falling down the opposite happens. But at any moment the sum of both energies is constant.


     
  3.  An object is dropped from the top of a high building and falls freely to the ground. Which one of the graphs below best represents its potential energy \((Ep)\) as a function of the distance fallen by the object? 

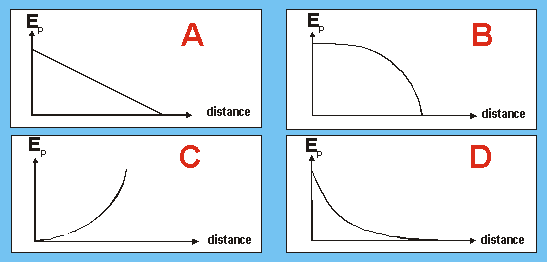
    Four possibilities for an object dropping from a high building. falling freely to the ground

    (A) A 
    (B) B 
    (C) C 
    (D) D 

    Correct = A 
    \(E_p = mgh\) is a linear function (straight line graph), which is only given in option A. Or in other words: the amount of potential energy decreases - on falling - by the same amount for equal distances/heights.


     
  4.  A large and a small sphere are released at the same time from the same height above the ground. Which one of the following quantities associated with the spheres will be the same for both after 1 second, if frictional effects are ignored? 

    (A) speed 
    (B) momentum 
    (C) potential energy 
    (D) kinetic energy 

    Correct = A
    Both spheres are exposed to the same acceleration (acceleration due to gravity) hence they develop the same speed in equal time intervals.


     
  5.  Which one of the following expressions has the same units as power? 

    (A) force x distance 
    (B) work x time 
    (C) force x acceleration 
    (D) force x velocity 

    Correct = D 
    The beautiful mathematics of units. Power = work done / time taken = force x displacement / time {\(\text N \cdot \text{m/s}\)}, which is given in option D.


     
  6.  A person lifts a heavy load to a vertical height of \(2.0\; \text m\) in \(3 \; \text{seconds}.\) If they had done this more slowly in \(6 \; \text{seconds}, \) the work on the load would have been: 

    (A) twice as great 
    (B) four times as great 
    (C) the same 
    (D) half as great 

    Correct = C 
    Remember, work does not depend on time (but power does), so the correct answer is option C.


     
  7.  At what height above the ground must a mass of \(10\; \text{kg}\) be to have a potential energy equal in value to the kinetic energy possessed by a mass of \(10\; \text{kg}\) moving with a velocity of \(20\; \text{m/s}\)? 

    (A) \(10\; \text m\) 
    (B) \(20\; \text m\) 
    (C) \(5 0\; \text m\) 
    (D) \(100\; \text m\) 

    Correct = B 
    \(E_k\) of a body of mass \(10\; \text{kg}\) with speed \(20\; \text{m/s} = 1/2\; \text mv^2 = 1/2 ·10·(20·20) = 5 · 400 = 2000\; \text J. E_p = m·g·h » h = E_p/m·g = 2000/100 = 20\; \text m.\)


     
  8.  A girl runs up one flight of steps. Which one of the following factors does not affect the work done by the girl against gravity? 

    (A) mass of the girl 
    (B) height of the steps 
    (C) speed of the girl 
    (D) acceleration due to gravity 

    Correct = C
    See also Question 6, the work done by the girl does not depend on the time taken to run up the flight of stairs, hence the speed does not matter. Or: \(E_p = mgh,\) mass \(m\) referred to in option A, height \(h\) referred to in option B and force due to gravity in option D.


     
  9.  A girl weighing \(400\; \text N\) runs up the a flight of stairs \(\text{(height 5 m)}\) in a time of \(4\; \text{seconds.}\) Her rate of working against gravity is ... 

    (A) \(320\; W\) 
    (B) \(400\; W\) 
    (C) \(500\; W\) 
    (D) \(2000\; W\) 

    Correct = C 
    Rate of work against gravity is power. \(P = 400·5/4 = 500W.\)


     
  10. A stone dropped from the top of a \(80\; \text m\) high building strikes the ground at \(40\; \text{m/s}\) after falling for \(4\; \text{seconds.}\) The stone's potential energy with respect to the ground is equal to its kinetic energy … 

    (A) at the moment of impact. 
    (B) 2 seconds after the stone is released. 
    (C) after the stone has fallen \(40\; \text m. \)
    (D) when the stone is moving at \(20\; \text{m/s.}\) 

    Correct = C
    A badly phrased question. Let us look at it this way. The stone has \(E_p= mgh = \text m·10·80 = 800\; \text m\) at the top of the building. When does it \(E_k\) equals this value? \(E_k= E_p = 800\; \text m = 1/2\; \text mv^2.\) Hence \(1600 = v^2 \)     or \(40 \; \text{m/s}.\)