Equations of Motion I
- A motorcycle accelerates from \(10\; \text{m/s}\) to \(25\; \text {m/s}\) in 5 seconds. What is the average acceleration of the bike?
(A) \(3\; \text{m/s}^2\)
(B) \(5\; \text{m/s}^2\)
(C) \(15 \; \text{m/s}^2\)
(D) \(25\; \text{m/s}^2\)Correct = A
Option A since acceleration = change of velocity per time = \(15\; \text {km/h}\) divided by \(5\; \text s=3\; \text {m/s}^2\)
- A ball is thrown vertically into the air and when it returns after an interval of 2 seconds, it is caught. Which one of the following statements is true if the acceleration due to gravity is \(10\; \text{m/s}^2\) and air resistance can be neglected:
(A) The acceleration at the top of its flight is \(10\; \text {m/s}^2.\)
(B) The time taken for the descending motion does not equal the time taken for the ascending motion.
(C) The maximum height it reaches does not depend on the force of gravity.
(D) The acceleration after it leaves the hand is \(10\; \text {m/s}^2\) downwards.Correct = D
This type of question shows up again and again. Remember: the moment an object is in the air the acceleration is \(10\; \text {m/s}^2\) with direction down, towards centre of the Earth. This is a result of the fact that in falling bodies the horizontal and vertical components of motion are independent of each other.
- A ball is thrown vertically up from the top of a building and the graph to the right shows the variation of its velocity with time up to the 5th second.
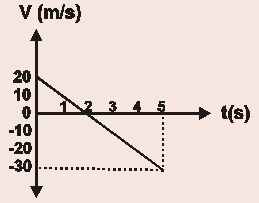
At the end of its journey (as shown by the graph) the ball is …
(A) back at its point of projection.
(B) \(25\; \text m\) from the point of projection and moving downwards.
(C) \(45\; \text m\) from the point of projection and moving downwards.
(D) \(25\; \text m\) from the point of projection and moving upwards.Correct = B
It is clear that options A and D do not make a lot of sense. But is it B or C? This is a tricky question. You might tend to go for C, arguing that since at the top of the motion of an object thrown vertiaclly up velocity is zero, hence distance covered in 3 seconds is \(45\; \text m (\text s=1/2\;gt^2).\) However, the ball did start its journey with an initial velocity of \(20\; \text {m/s}^2\) up. Hence:\( \text s=ut + 1/2\; gt^2= -150 + 125 =\) (- direction down) \(25\; \text m.\)
- Which of the given \(velocity : time\) graphs (A, B, C, D) matches the given \(acceleration : time\) graph which you see below?
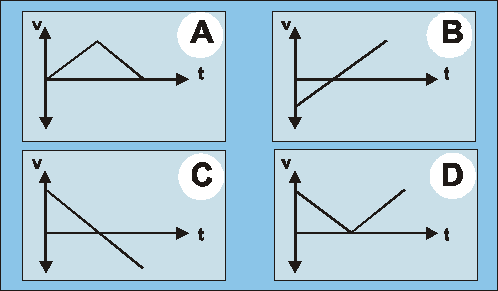
Velocity : Time 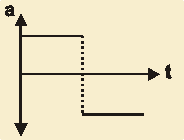
Acceleration : Time
(A) A
(B) B
(C) C
(D) DCorrect = A
The given graph represents a motion with a positive constant acceleration (=increase in velocity) and thereafter a constant negative acceleration (=decrease in velocity). So which graph shows a positive and negative acceleration? B and C are out since they represent a constant acceleration. In B the gradient is positive hence a positive acceleration, C shows a constantly slowing down motion. But is it A or B? First we look for a positive acceleration, which is only in A the case, followed by a deceleration. Again only A fulfils this criteria.
- A ball is thrown vertically upwards. If air resistance is ignored, the ball will move with constant …
(A) velocity
(B) momentum
(C) acceleration
(D) potential energyCorrect = C
Compare with question 2. Again the same scenario: if object is airborne the acceleration is \(g\)
- A ball is thrown vertically upwards. Ignore air resistance. Take the upward motion as positive. Which one of the following graphs represents the velocity of the ball as a function of time?
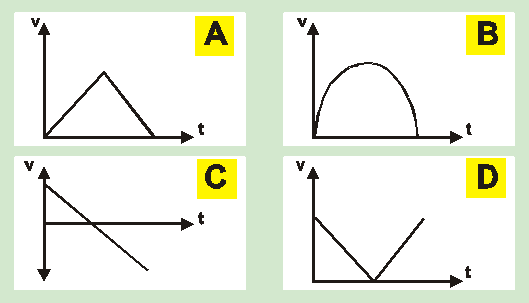
(A) A
(B) B
(C) C
(D) DCorrect = C
Acceleration is \(-10\; \text{m/s}^2\) hence we have to look for a graph which has a constant negative gradient. Only C does so.
- Two heavy metal spheres \(P\) and \(Q\) are simultaneously dropped from the same height as shown in the diagram below. The sphere \(P\) is much smaller than sphere \(Q\). Ignore the effect of air resistance.
Which one of the following is the correct observation and possible reason for what happens?
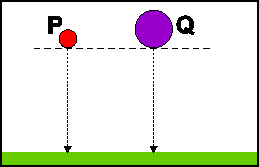
Answer observation possible reason (A) they reach the floor simultaneously gravitational forces are equal for both spheres (B) they reach the floor simultaneously the gravitational acceleration is the same for both (C) \(P\) reaches the floor first smaller objects always fall 'faster' than bigger ones (D) \(Q\) reaches the floor first the earth's force of gravity is greater on the heavier object Correct = B
For A: correct observation but the conclusion goes astray. The gravitational forces (weights of spheres) are not equal. C and D are full of mis- and preconceptions regarding falling objects (see the document Aristotle versus Galileo which you will find under teaching resources Physics on this website). Provided frictional forces are not considered B says it all.
- A ball falls vertically from rest from a high cliff from point A as shown in the sketch. At point B the ball reaches its terminal velocity. While the ball is falling from B to C, its kinetic energy will ...
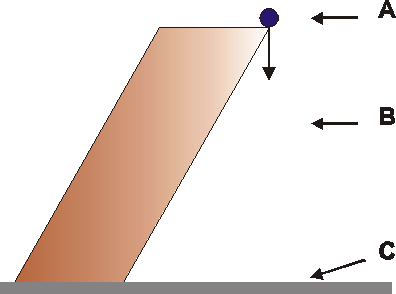
(A) be zero
(B) increase
(C) decrease
(D) remain constantCorrect = D
\(\text {Kinetic energy} =1/2\; mv^2.\) After a falling body has reached its terminal velocity the frictional forces due to air resistance are balanced by the acceleration due to gravity (remember: no resultant force, no acceleration). Hence no change in velocity/speed between B and C; which results in a constant kinetic energy after the ball has passed point B.
- A rock is thrown vertically upwards with a speed '\(v\)' from the edge of a cliff. At the same moment, a second rock is thrown vertically downwards with the same initial speed '\(v\)'. Which of the following statements regarding the motion of the rocks is true (ignore air resistance.)?
(A) The rock which was thrown upwards reaches the bottom of the cliff with a higher velocity.
(B) The rock which was thrown downwards reaches the bottom of the cliff with a higher velocity.
(C) Both rocks reach the bottom of the cliff with the same velocity at the same time.
(D) Both rocks reach the bottom of the cliff with the same velocity but at different times.Correct = D
Option D is the good one. This is a dangerous question because in many similar sounding questions so often the objects hit the ground at the same time due to the same gravitational acceleration (see also question 7). But in this case the initial velocity of the stone which was dropped was not zero hence it will reach the ground first.
- The path \(PQR\) of a soccer ball kicked from a point \(P\) on the ground is shown in the diagram at the right. At point \(Q,\) the ball is at its maximum height.
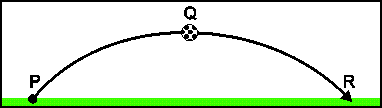
Which ONE of the following vectors may represent the acceleration due to gravity of the ball at point \(Q\)?
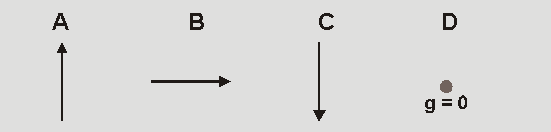
(A) A
(B) B
(C) C
(D) DCorrect = C
Acceleration due to gravity always pointing towards centre of Earth. See also questions 2, 5, and 7.







