Momentum

  1. A cricket ball of mass '\(m\)' travelling at a speed of '\(v\)', is struck back in the opposite direction with the same speed '\(v\)'. The magnitude of the change in momentum of the ball is… 

    (A) \(2\; mv \)
    (B) \(mv^2\) 
    (C) \(mv\) 
    (D) \(0\) 

    Correct = A

    Since \(v=u\) we can say that change in momentum \(= m(v - u) = m(v + v) = 2\;mv.\) Or if we take u as positive: change in momentum \(= m (-v +-u)= -2\;v.\) Hence it was asked for the magnitude of the change of momentum it is still \(=2\;mv.\)


     
  2.  A moving object \(X\) has a mass \(m\) and speed \(v.\) Another moving object \(Y\) will have twice the momentum of \(X\) if it has a mass and velocity of:

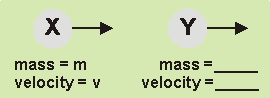
    Diagram of a moving object X and another moving object Y
     
    Answer Mass Velocity
    (A) \(1/2\; m\) \(1/2\; v\)
    (B) \(1/2\; m\) \(2\; v\)
    (C) \(4\; m\) \(1/2\; v\)
    (D) \(4\; m\) \(2\; v\)
     

    Correct = C

    Object \(X\) has momentum of \(p=mv.\) Twice the momentum is \(2mv.\) Where in the table do we find the factor of \(\text{velocity} \times \text{mass} = 2mv?\) Only in C we get \(2mv\) after multiplication.

     
  3. A soccer ball of mass \(1\; \text {kg}\) strikes a wall at right angles with a velocity of \(2\; \text {m/s}\) as shown in the sketch. It bounces back with a velocity of \(1.5\; \text {m/s}. \)

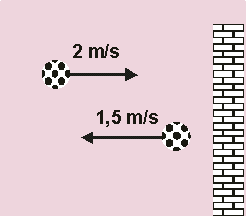
    Diagram of a soccer ball striking a wall and bouncing back

    The impulse of the wall on the ball (in \(\text{kg.m/s}\)) is ... 

    (A) \(0.5\) to the right 
    (B) \(0.5\) to the left 
    (C) \(3.5\) to the right 
    (D) \(3.5\) to the left 

    Correct = D

    Similar to question 1 since impulse = change in momentum. The magnitude we get from \(u=+2\;m/s\) -take towards wall as positive-; \(v=-1.5\; \text{m/s}: \text{impulse} = \text m(-2 -+1.5)= -3.5\; \text m.\) Negative since direction is away from wall which is to the left.


     
  4. Two trolleys \(A\) and \(B\) are moving towards one another as shown in the diagram at the right. They collide and come to rest at the point of impact.

    From this observation we can conclude that the trolleys have …    

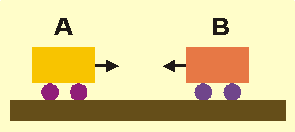
    Two trolleys A and B are moving towards one another

    (A) equal masses. 
    (B) were moving with equal and opposite momentum. 
    (C) were moving with equal and opposite velocities. 
    (D) were moving with equal kinetic energies. 

    Correct = B

    Only having equal but opposite momentum brings trolleys to a stop after impact. Same masses does not consider velocity (in A) and same velocity does not consider mass (in C). One might tend to think that eqal kinetic energies stops them, but because of \(v^2\) it is not the case.


     
  5. A snooker ball \(A\) moves at a velocity of \(6\; \text {m/s}\) and collides with two identical snooker balls \(B\) and \(C,\) as shown in the sketch. Ignore all friction. 

    After the collision …  

    A snooker ball A moves at a velocity of 6 m/s and collides with two identical snooker balls B and C

    (A) balls \(A\) and \(B\) are stationary and \(C\) moves at \(6\; \text {m/s}.\) 
    (B) balls \(A\) and \(B\) are stationary and \(C\) moves at \(3\; \text {m/s}.\) 
    (C) ball \(A\) is stationary and \(B\) and \(C\) move at \(3\; \text {m/s}.\)
    (D) all three balls move at \(2\; \text {m/s}.\) 

    Correct = A

    Conservation of momentum. Momentum of \(A\) is transferred via B to C since \(A,\) \(B\) and \(C\) were positioned in a straight line (this should have been stated in the question!). Think of the collision as follows: \(A\) causes a small deformation in \(B,\) this deformation travels through the material, meets \(C\) at the boundary, passes deformation on to \(C,\) but \(C\) cannot pass it to another body, hence \(C\) starts to move at velocity at which \(A\) hits \(B\) (frictional forces ignored).


     
  6. The diagram at the right shows two blocks \(A\) and \(B,\) which are connected by a rubber band. The mass of \(A\) is twice the mass of \(B.\) 

    The two blocks are pulled apart on a smooth horizontal surface and released simultaneously. When they are released, the blocks collide and …  

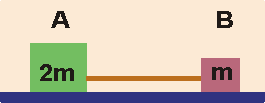
    diagram showing two blocks A and B, which are connected by a rubber band

    (A) both move to the right. 
    (B) both move to the left.  
    (C) both remain at rest. 
    (D) block \(A\) remains at rest and \(B\) moves to the right. 

    Correct = C

    This type of question is famous and appears often in disguise. Both remain a rest after colliding because they had equal but opposite momentum before the impact. The stretched rubber band does not accelerate both blocks in the same way. Of course the smaller block \(B\) gains a higher velocity. However, it has the same momentum as \(A\) since it has a smaller mass.


     
  7. Newton's second law of motion states: 

    (A) For every action there is an equal and opposite reaction. 
    (B) A body will remain at rest unless acted upon by an unbalanced force. 
    (C) The force acting on a body equals the rate of change of momentum.  
    (D) A body will move with uniform motion in a straight line, unless acted upon by an unbalanced force. 

    Correct = C

    Option C is Newton II in its original form. We often refer to Newton II only as \(F = ma.\) However, we can rewrite it to: \(F = m(v - u) / \text{time} = mv - mu / \text{time},\) which is exactly what statement C says.


     
  8. Two vehicles move towards each other on a frictionless road as shown in the sketch below. The two cars collide and immediately come to a standstill. 

    Two vehicles move towards each other on a frictionless road

    During the collision, the total momentum of the two vehicles will … 

    (A) decrease. 
    (B) stay constant. 
    (C) firstly increase and then decrease. 
    (D) firstly decrease and then increase. 

    Correct = B

    Only option B is in accordance with the law of conservation of momentum: total momentum before a collision = total momentum after a collision.


     
  9. An open truck is moving horizontally with a constant velocity along a frictionless track underneath a grain bin. Grain, falling vertically down, now starts falling into the truck, partly filling it as it moves along. What will happen to the momentum of the truck accumulating grain? 

    (A) It will decrease. 
    (B) It will increase. 
    (C) It will first increase and then decrease. 
    (D) It will stay the same. 

    Correct = D

    Very similar to the previous question. The vertically down falling grain does not have a component of its velocity in the direction of the moving truck so it does not contribute to the velocity of the truck. However, the grain makes the truck not only heavier but also slower and as a result the momentum stays the same.


     
  10. Two trolleys, \(X\) and \(Y,\) of masses \(4\; \text {kg}\) and \(6\; \text {kg}\) respectively, are held stationary on a horizontal surface with a spring compressed between them. Two barriers are situated equidistant from each trolley as shown in the diagram below. 

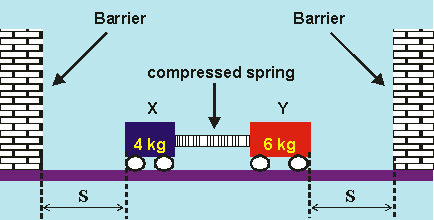
    Two trolleys, X and Y, of masses 4 kg and 6 kg respectively, are held stationary on a horizontal surface with a spring compressed between them. Two barriers are situated equidistant from each trolley.

    When the spring is released … 

    (A) trolley \(X\) will strike the barriers first. 
    (B) trolley \(Y\) will strike the barrier first.  
    (C) both trolleys will strike the barrier at the same time. 
    (D) the final momentum is zero and therefore the trolleys will not reach the barrier. 

    Correct = A

    Do not jump for the may be tempting option C. The question is similar to No.6. The stored energy of the spring causes greater acceleration to the trolley with less mass. Hence trolley \(X\) will hit the wall first. Alternatively you can look at it in this way: momentum before release = zero = momentum after release. For the momentum to be the same but in opposite directions, the trolley with smaller mass must move at a higher velocity and as a result must hit the barrier before trolley \(Y.\)