Equations of Motion 2

  1. A hunter points a dart directly at a monkey sitting on a tree. However, just as the hunter fires the dart the monkey drops from the branch. The dart will ... 

    (A) Strike the monkey. 
    (B) Pass over the monkey. 
    (C) Pass below the monkey. 
    (D) More information is required to answer the question. 

    Correct = A

    They hit the ground at the same time since vertical component of motion is independent of horizontal component. This question appears in many disguises. But be careful not to mistake it with a type of question, were the initial velocity in vertical direction is not zero: see question 9 in multiple choice test 1 on Equations of Motion 1.


     
  2.  A parachutist is descending with uniform velocity. This indicates that he is experiencing … 

    (A) no forces at all 
    (B) zero resultant force 
    (C) a downward resultant force 
    (D) an upward resultant force 

    Correct = B

    When gravitational force (weight of parachutist) is balanced by frictional force (air friction) acceleration becomes zero and the falling object has reached its terminal velocity which is of course uniform. In parachuting it is said to be around \(180\; \text {km/hr}\) when the brave person is outstretched to max. air resistance.


     
  3. A motorcycle accelerates uniformly from rest along a straight road, reaching a speed of \(200\; \text {km/h}\) after \(10.0\) seconds. At what stage during the motion does the bike's speedometer needle pass the \(100\; \text {km/h}\) mark?

    (A) halfway along the road 
    (B) \(5.0\) seconds after starting 
    (C) some distance after the halfway mark 
    (D) some time before \(5.0\) seconds 

    Correct = B

    Reaching a speed of \(200\; \text {km/hr}\) after 10 seconds requires an acceleration of \(20\; \text{m.s}^{-2}.\) Hence with an acceleration of \(20\; \text{m.s}^{-2}\) it takes 5 seconds for the bike to reach a speed of \(100\; \text {km/hr}.\)


     
  4. Consider the following velocity-time graph of a car starting from rest in a straight line. At what time of the movement is the object the furthest from its starting point? 

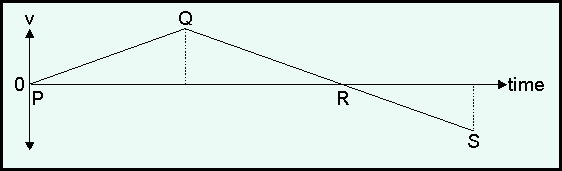
    velocity-time graph of a car starting from rest in a straight line

    (A) P 
    (B) Q 
    (C) R 
    (D) S 

    Correct = C

    The given graph represents a motion with a positive constant acceleration (= increase in velocity until the car reaches point \(Q\)) and thereafter a constant negative acceleration (= decrease in velocity until point \(R\)). However, the direction of motion remains the same. Hence the object is furthest away from its starting point at point \(R\). After \(R\) it turns and moves back towards its starting point.


     
  5.  A girl, standing on a bridge, throws a metal sphere vertically downwards as hard as she can. Which statement concerning the acceleration of the stone after it has left her hand is true? (Ignore any effects of air resistance.) 

    (A) The sphere's acceleration is equal to "g". 
    (B) The sphere's acceleration is greater than "g". 
    (C) The sphere's acceleration is less than "g". 
    (D) The sphere's acceleration is at first greater than "g", then becomes equal to "g". 

    Correct = A

    Again the same scenario: an if object is airborne the acceleration is g and nothing but g.


     
  6.  How far does a stone fall in \(1.0\; \text s\) when dropped on earth, disregarding any air resistance? 

    (A) 1 m 
    (B) 5 m 
    (C) 10 
    (D) 20 

    Correct = B

    Acceleration is 10m/s2, time is 1 second, hence we can use the following equation of motion: 

    \(\text s = ½\; g\; t^2 \\ \text s = ½ ·10\; \text {m/s}^2 · 1\; \text s^2 \\ ​​​​​​​\text s = 5\; \text m\)



    Question 7 and 8 refer to the diagram below:
     
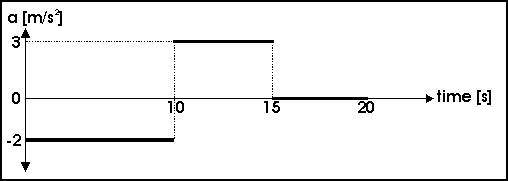
    A car is moving on a straight, horizontal road at 30 m.s-1 in an easterly direction. The acceleration of the car for the following 20 s is shown as a function of time.
     A car is moving on a straight, horizontal road at \(30\; \text{m.s}^{-1}\) in an easterly direction. The acceleration of the car for the following \(20\; \text s\) is shown in the graph as a function of time. 


     
  7. The velocity of the car is … 

    (A) \(5\; \text {m.s}^{-1}\) west 
    (B) \(25\; \text{ m.s}^{-1} \)west 
    (C) \(5\; \text{ m.s}^{-1}\) east 
    (D) \(25\; \text {m.s}^{-1}\) east 

    Correct = D

    Car moving at \(30\; \text {m/s}.\) Decelerates for 10 seconds with negative \(2 \; \text {m.s}^2\): velocity has decreased to \(10\; \text{m/s}.\) Then acceleration with \(a=3\; \text{m.s}^2\) increases velocity to \(25\; \text{m/s}\) (\(10\; \text{m/s} + 15\; \text{m/s}\)). After 15 seconds no further change in velocity, hence car is travelling at \(25\; \text{m/s}\) east.


     
  8.  During the 20 seconds when is the car stationary? 

    (A) from 0 to 10 seconds 
    (B) from 10 to 15 seconds 
    (C) from 15 to 20 seconds 
    (D) never 

    Correct = D

    That was easy to see. 


     
  9.  Which of the following will not effect on the acceleration of a falling object on planet earth? 

    (A) Height of the object above sea level. 
    (B) Distance between centre of the earth and the object. 
    (C) Mass of the object. 
    (D) Mass of the earth. 

    Correct = C

    \(A,\; B\) and \(C\) have all an influence on acceleration due to gravity on the earth (and of course on other planets as well!). See also question 7, Equations of motion I.


     
  10.  A parachutist lands on the ground at a speed of \(6\; \text {m/s}.\) The height from which a free-falling object will have to fall to reach the same speed is … 

    (A) \(0.30\; \text m\) 
    (B) \(1.80\; \text m\)  
    (C) \(3.60\; \text m\) 
    (D) \(60\; \text m\) 

    Correct = B

    Apply the following equation of motion: 
    \(v^2 = u^2 + 2as \\ 36 = 0 + 2·10·x \\ 36/20 = 18/10 = 1.8 \\ \text {height} = 1.8\; \text m.\)