Problem 12-22 Simple circuit - Part 5 - B

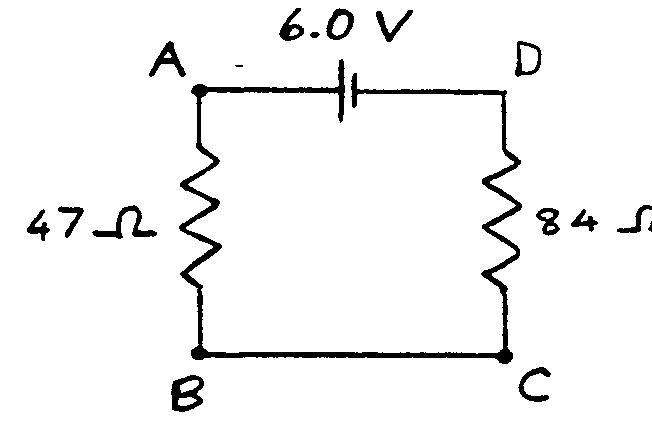
In the figure, what are
(a) the current through the \(47\; \Omega\) resistor?
(b) the direction of the current through the \(47\; \Omega\) resistor?
(c) the potential difference \(V_A - V_B\)?  \(V_B - V_A\)?
(d) the voltage across the \(84\;  \Omega\)  resistor?
(e) the potential at point \(C\), if we define the potential at the negative terminal of the battery to be zero?

Accumulated Solution

\(I = V/R \\ I = V/R = 6.0/131 = 0.046\; \text{A}    \quad  \text{(answer to part (a))} \\ \text{Current flows + to -, therefore A to B } \quad \text{(answer to part (b))} \\ \Delta V = IR = 0.046 \times 47 = 2.2\; V\)

Correct. Current flows from high potential to low so B is lower than A.

\(V_B - V_A = -2.2 \;V  \quad    \text{(answer to part (c))}\)

The potential difference across the \(84\; \Omega\) resistor is:

(A)   \(84 \;V\)

(B)   \(3.8\; V\)

(C)   \(2.2\; V\)