Amplitude, Period and Frequency

Here is a ball moving back and forth with simple harmonic motion (SHM):

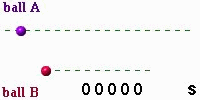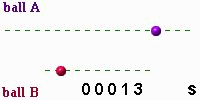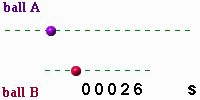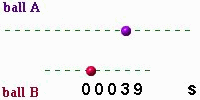
ball moving back and forth with simple harmonic motion

Its position x as a function of time t is:

x(t)=A⋅cos(2⋅π⋅tT)

where A is the amplitude of motion: the distance from the centre of motion to either extreme

T is the period of motion: the time for one complete cycle of the motion.

Questions

Which ball has a larger amplitude?

Ball A or Ball B

 

Which ball has a longer period?

Ball A or Ball B

Ball A - Correct!
Ball B - No. That is not correct

 

What is the period of Ball B?

A) 4.0s
B) 8.0s
C) 12 s
D) 16s

A) 4.0s - No. The period is the time for one full oscillation.
B) 8.0s - No. The period is the time for one full oscillation.
C) 12 s - Correct!
D) 16s - No. The period is the time for one full oscillation.

 

The frequency of motion, f, is the rate of repetition of the motion -- the number of cycles per unit time. There is a simple relation between frequency and period: f=T−1

What is the frequency of ball B (recall, the period is 12s)?

A) 0.0625 Hz
B) 0.0833 Hz
C) 0.125 Hz
D) 0.250 Hz

A) 0.0625 Hz - No. Remember f=1/T
B) 0.0833 Hz - Correct!
C) 0.125 Hz  - No. Remember f=1/T
D) 0.250 Hz  - No. Remember f=1/T

 

Angular frequency is the rotational analogy to frequency. Represented as , and is the rate of change of an angle when something is moving in a circular orbit. This is the usual frequency (measured in cycles per second), converted to radians per second. That is ω=2π/T=2πf

Which ball has the larger angular frequency?

Ball A or Ball B

Ball A - No. ω is proportional to f

Ball B - Correct!

 

What is ball B's angular frequency?

A) 0.125πrads−1
B) 0.167πrads−1
C) 0.250πrads−1
D) 0.500πrads−1

A) 0.125πrads−1 - No. ω=2pf
B) 0.167πrads−1 - Correct!
C) 0.250πrads−1 -  No. ω=2pf
D) 0.500πrads−1 -  No. ω=2pf

 

Position-time graph of a moving piston
Figure 1: position-time graph of a piston moving in and out.

From this graph, find the following:

1. Amplitude (A) 2. period (T) 3. frequency (f) 4. angular frequency (ω)
A) 20 cm A) 0.20 s A) 0.20 Hz A) 0.20πrads−1
B) 1.0 cm B) 1.0 s B) 1.0 Hz B) 1.0πrads−1
C) 5.0 cm C) 5.0 s C) 5.0 Hz C) 5.0πrads−1
D) 10 cm D) 10 s D) 10 Hz D) 10πrads−1
  1. amplitude (A):
    A) 20 cm - No. It is not the distance from a crest to a trough.
    B) 1.0 cm - No. That is not correct.
    C) 5.0 cm - No. That is not correct.
    D) 10 cm - Correct!
     
  2. period (T):
    A) 0.20 s - Correct!
    B) 1.0 s - No. The period is the time for one full oscillation.
    C) 5.0 s - No. The period is the time for one full oscillation.
    D) 10 s - No. The period is the time for one full oscillation.
     
  3. frequency (f):
    A) 0.20 Hz - No. The frequency is 1/T
    B) 1.0 Hz - No. The frequency is 1/T
    C) 5.0 Hz - Correct!
    D) 10 Hz - No. The frequency is 1/T
     
  4. angular frequency (ω):
    A) 0.20πrads−1 - No. ω=2πf
    B) 1.0πrads−1 - No. ω=2πf
    C) 5.0πrads−1 - No. ω=2πf
    D) 10πrads−1 - Correct!