Velocity and Acceleration

Once you know the position of the oscillator for all times, you can work out the velocity and acceleration functions.

\(x(t) = A \cos (\omega t + \phi)\)

The velocity is the time derivative of the position so:
\(v(t) = -A \omega \sin (\omega t + \phi)\)

The change from cos to sin means that the velocity is 90o out of phase with the displacement-when x = 0 the velocity is a maximum and when x is a maximum v = 0. This is seen nicely in the page on the connection between SHM and circular motion.

The acceleration is the time derivative of the velocity so:
\(a(t) = -A \omega^2 \cos (\omega t + \phi)\)

Notice also from the preceding that:

\(a(t) = -\omega ^2x\)   The acceleration is exactly out of phase with the displacement. This can also be seen in the page on the connection between SHM and circular motion.

Watch the oscillating duck. Let's consider velocity now. Remember that velocity is a vector, and so has both negative and positive values.

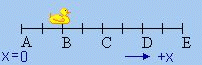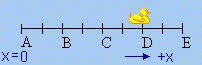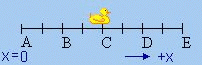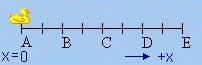
Where does the magnitude of \(v(t)\) have a maximum value?
A
B
C
D
E   

Where does \(v(t) = 0\)?
A
B
C
D
E

Watch the oscillating duck again. Let's look at acceleration. Again, remember that acceleration is a vector.

Where does \(a(t)\) have a maximum value?
A
B
C
D
E   

Where does \(a(t) = 0\)?
A
B
C
D
E

You now know several parameters that are used to describe SHM:

• amplitude \((A)\)
• period \((T)\)
• frequency \((f)\)
• angular frequency \((\omega)\)
• initial phase \((\phi)\)
• maximum velocity \((v(t)_{max})\) and
• maximum acceleration \((a(t)_{max})\)

There are many relations among these parameters.

One minimum set of parameters to completely specify the motion is:

amplitude \((A)\)
angular frequency \((\omega)\)
initial phase \((\phi)\)

You are already familiar with this set, which is used in:

\(x(t) = A \cos (\omega t + \phi)\)

The trick in solving SHM problems is to take the given information, and use it to extract \(A\), \(\omega\) and \(\phi\).

Once you have \(A\), \(\omega\) and \(\phi\), you can calculate anything.