Biophysics Textbook Questions - Chapter 9

A lab technician is centrifuging a blood sample at an angular speed of 3000 rpm (revolutions per minute). If the radius of the circular path followed by the sample is 0.15 m, find the speed of the sample in m s.

\(a_c = \frac{v^2}{r},  \text{but}\; v = \frac{2\pi r}{T} \text{and} \; T = \frac{1}{f}\) (as in Exercise 9-1)

\(\begin {align} \therefore a_c = 4 \pi ^2 \;r\; f^2 \\ \therefore f= \frac{1}{2 \pi}\sqrt{\frac{a_c}{r}} & = \frac{1}{2 \pi} \sqrt{\frac{6.00 \times 10^3(9.80\; \mathrm{m/s^2)}}{0.0500\; \mathrm{m}}} \\ & = 172.6\; \mathrm{\frac{rev}{s}} \times \frac{60.0\;\mathrm{s}}{1\;\mathrm{min}}\\ &= 1.04 \times 10^4 \mathrm{\frac{rev}{min}} \end{align}\)

As in Exercise 9-2, \(a_c = \frac{v^2}{r}, \text{but}\; v = \frac{2 \pi r}{T} \;\text{and} \;T = \frac{1}{f}\)

\(\begin {align} \therefore a_c = 4 \pi ^2 \;r \;f^2 \\ \therefore f = \frac{1}{2\pi}\sqrt{\frac{a_c}{r}} & = \mathrm{\frac{1}{2\pi}\sqrt{\frac{9.80\;m/s^2}{1.00\times 10^3\;m}}} \\ & = \mathrm{0.0158\; Hz\quad (0.0157_6\;Hz)} \end {align}\)

\(T = \frac{1}{f}= 63.5\; \mathrm{s} \quad(63.4_7\;\mathrm{s})\\ v = \frac{2\pi r}{T}= \frac{2\pi (1.00 \times 10^3\; \mathrm{m})}{63.4_7\; \mathrm{s}}= 99.0\; \mathrm{m/s}\)

\(\begin {align} \sum F &= m\;a_c \\ \therefore T&= \mathrm{m}\frac{v^2}{r}\\ \therefore v &= \sqrt{\frac{rT}{\mathrm{m}}}\\ &= \mathrm{\sqrt{\frac{(0.850\;m)(575\;N)}{0.950\;kg}}}\\ &= \mathrm{22.7\; m/s} \end {align}\)

\(\sum F= \mathrm{m}\;a_c \\ \therefore F _{friction}= \mathrm{m} \frac{v^2}{r}\)

On the verge of slipping, \(F_{friction}= F_{max}= \mu_s\;\mathrm{N}\)

The only vertical forcers are:

\(\mathrm{m \overrightarrow g \; (down) \;and \; \overrightarrow N \; (up)\; \Rightarrow \;N = m\;g} \\ \therefore \mu_s \; \mathrm{m\;g} = \mathrm {m} \; \frac{v^2}{r} \\ \therefore \mu_s = \frac{v^2}{r\;g}= \frac{(27.0\; \mathrm{m/s})^2}{(320\; \mathrm{m})(9.80\; \mathrm{m/s^2})}= 0.232\)

If \(r\) is smaller, then from \(\mu_s = \frac{v^2}{r\;g} , \mu_s\) would have to be larger, i.e., it would have to increase.

FBD for skier:

\(\begin {align} \mathrm{\sum F_y = m\;a_y} &= \mathrm{m\;a_c \quad, where\;m = \frac{510\;N}{9.80\;m/s^2}= 52.0\;kg \quad (52.04\;kg)}\\ \mathrm{\therefore N-m-g} & = \mathrm{m\frac{v^2}{r}}\\ \mathrm{\therefore N} &= \mathrm{m\bigg( g+ \frac{v^2}{r} \bigg)} \\ &= \mathrm{52.0_4 \bigg(9.80 + \frac{(15.0)^2}{28.5} \bigg)}\\ &= \mathrm{921\;N} \end{align}\)

FBD for scafffold:

\(\mathrm{\sum T = 0, about \; P \quad \uparrow+\\ \therefore (T_1)(0)- (W_m)(1.00\;m)- (W_s)(2.00\;m)+(T-2)(4.00\;m)= 0}\)

\(\begin {align} \mathrm{\therefore\; T_2} & = \mathrm{\frac{W_m+2.00\;W_s}{4.00}}\\ &= \mathrm{\frac{(100)(9.80)+ 2.00 (750)}{4.00}}\\ &= \mathrm{620\;N \quad 620.0\;N} \end {align}\)

\(\mathrm{\uparrow+y\; \sum F_y = m\;a_y \\ \therefore T_1+T_2 - W_m-W_s= 0}\\ \begin {align} \mathrm{\therefore T_1} & = \mathrm{W_m+W_s - T_2} \\ &= \mathrm{(100\;kg)(9.80\;m/s^2)+(750\;N)-(620\;N)} \\ &= \mathrm{1.11 \times 10^3 \; N} \end {align}\)

A teeter-totter is \(\mathrm{20\; kg}\) in mass. Assume it is a uniform plank of length \(\mathrm{2 \;m}\). The pivot point is placed \(\mathrm{0.2 \;m}\) from the midpoint. What weight must be added to the short end to balance the teeter-totter?

(Hint: Think a moment about the pivot - the uniform plank can be assumed to be a single weight concentrated at its midpoint. Can you justify this?)

There are 3 vertical forces here, of which we know only one (the weight of the plank). I hope you realize that if you take moments about the pivot point you will get an equation that does not contain one of the unknowns(the upward force through the pivot point). The equation will contain the only other unknown, which is the weight of the mass added to the short end.

First, add to the diagram the vectors representing the two downward forces. Also indicate their distances from the pivot point.

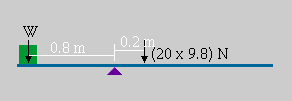
Now use the principle of rotational equilibrium and take moments about the pivot point to solve for W.

You should have:

\(\mathrm{  W \times 0.8\;m = (20 \times 9.8) \times 0.2\;m \\          W = 49 \;N}\)

FBD for plank:

FBD for arm.

For static equilibrium, \(\mathrm{\Sigma \tau = 0}\) about the pivot point O.

\(\mathrm{\therefore T\bigg ( \frac{OC}{2}\sin\theta\bigg) -w (OC \sin \theta)\\ \therefore T = 2w \frac{sin \theta}{\sin \emptyset}}\)

\(\mathrm{\tau \; due \; to\; \overrightarrow w, \; about \; K, \; is:}\)

\(\begin {align} \mathrm{\tau} & = \mathrm{- (m\;g)(d \; \sin\; 22.0^\circ)}\\ & = \mathrm{- (12.0\;kg)(9.80\; m/s^2)(0.600\;m)\sin \;22.0^\circ}\\ & = \mathrm{- 26.4\; N\cdot m } \end {align}\)

\(\mathrm{\sum \tau = 0 \; about \;P.\\ \therefore \; E\; (0)+ (T)(PA\; \sin \; 60.0^\circ)-w\;(PB)= 0 \\ \therefore \; T = \frac{w(PB)}{PA\sin 60.0^\circ}= \frac{150(40.0)}{3.00\; \sin \; 60.0^\circ}= 2.31 \times 10^3 \; N \quad (2.30_9\times 10^3 \; N)}\)

\(\mathrm{\underbrace {\sum F_x = 0} \; and\; \sum F_y = 0 \\ \therefore \; E_x - T \cos 60.0^\circ = 0 \\ \Rightarrow E_x = 1155\;N \\ \sum F_y = 0 \Rightarrow E_y + T \sin 60.0^\circ - w = 0\\ \Rightarrow E_y = -1850\; N}\)

\(\begin {align} \mathrm{\Rightarrow E} &= \mathrm{2.18\times 10^3 \;N} \\ \mathrm{\theta} &= \mathrm{58.0^\circ} \end {align}\)

\(\begin {align} \mathrm{Total \; \Delta \theta} & = \mathrm{ 2 \pi\; rad} \\ \mathrm{Total \; \Delta \theta} & = \mathrm{w_1\; \Delta t + w_2 \; \Delta t}\\ \mathrm{\therefore 2 \pi} & = \mathrm{1.67\times 10^{-3}\Delta t + 3.33 \times 10 ^{-3}\Delta t}\\ \mathrm{\Rightarrow \Delta t} & = \mathrm{1.25_9 \times 10^3 \times \frac{1\; min}{60.0 \; s}}\\ & = \mathrm{20.9 \; min.} \end {align}\)

(a)

\(\begin {align} \mathrm{\propto} & = \mathrm{2\pi \frac{rad}{s^2} \times \frac{1\; rev}{2 \pi \; rad}= 1.00 \frac{rev}{s^2}}\\ \mathrm{w_o} & = \mathrm{600 \frac{rev}{min}\times \frac{1\; min}{60.0\;s}= 10.0 \frac{rev}{s}}\\ \mathrm{w} & = \mathrm{w_o + \propto t}\\ &= \mathrm{10.0 \frac{rev}{s}+ \bigg( 1.00\; \frac{rev}{s^2}\bigg)(60.0\; s)}\\ & = \mathrm{70.0 \frac{rev}{s}\times \frac{60.0\;s}{1\; min}}\\ & = \mathrm{4.20 \times 10^3 \frac{rev}{min}} \end {align}\)

For \(\mathrm{rad/s}\) :\(\mathrm{w = 70.0 \frac{rev}{s} \times \frac{2 \pi \; rad}{1 \; rev}= 4.40 \times 10^2 \;rad/s}\)

(b)

\(\begin {align} \mathrm{\theta} & = \mathrm{w_ot+ \frac{1}{2}\propto t^2}\\ & = \mathrm{\bigg( 10.0 \frac{rev}{s} \bigg) (60.0\;s)+ \frac{1}{2} \bigg( 1.00 \frac{rev}{s^2} \bigg)(60.0\;s)^2} \\ & = \mathrm{2.40 \times 10^3\; rev} \end {align}\)

\(\begin {align} \mathrm{v} & = \mathrm{r\; w ; where\; w \; must\; be \; in\; rad/s } \\ \mathrm{\therefore \; v } & = \mathrm{0.900\; m \bigg ( 1.50 \frac{rev}{s} \times \frac{2 \pi rad}{1\; rev} \bigg)} \\ & = \mathrm{8.48 \; m/s} \end {align}\)

(a) \(\mathrm{v = r\;w = (0.850\;m)(10.0 \frac{rad}{s})= 8.50\;m/s}\)

(b)

\(\begin {align} \mathrm{w} & = \mathrm{w_o + \propto t} \\ \mathrm{\therefore\; \propto} & = \mathrm{\frac{w-w_o}{t}= \frac{(10.0-0)rad/s}{1.75\;s}= 5.71 \; rad/s^2} \end {align}\)

(a)

\(\begin {align} \mathrm{a_t} & = \mathrm{r \propto = (0.300\;m)(0.500\;rad/s^2)= 0.150\;m/s^2}\\ \mathrm{a_c} & = \mathrm{\frac{v_o{^2}}{r}= 0\;m/s^2 \quad (v_o = 0\;m/s)} \end {align}\)

(b)

\(\begin {align} \mathrm{\propto} & = \mathrm{constant \; \therefore \; a_ t = constant = 0.150\;m/s^2} \\ \mathrm{w^2} & = \mathrm{w_o{^2} + 2 \propto \theta} \\ & = \mathrm{ (0 \; rad/s)^2 + 2 (0.500 \frac{rad}{s^2})(240^\circ \times \frac{\pi \; rad}{180^\circ})}\\ \mathrm{\Rightarrow w } & = \mathrm{2.047 \; rad/s} \\ \mathrm{a_c} & = \mathrm{\frac{v^2}{r}= \frac{(wr)^2}{r}= w^2r = (2.04_7 \frac{rad}{s}^2)(0.300\;m)}\\ & = \mathrm{ 1.26 \; m/s^2} \end {align}\)

\(\mathrm{w^2 = w_o{^2}+ 2 \propto \theta \\ \therefore (3.20 \times 10^4)^2 = 0^2 + 2 \propto(2.13 \times 10^4)\\ \therefore\; \propto = 2.40_4 \times 10^4\; rad/s^2}\)

Then, \(\mathrm{w_1 = w_o + \propto t, }\)

\(\mathrm{\therefore t_1 = \frac{w_1-w_o}{\propto} = \frac{(7.55\times 10^4 rad/s)}{2.40 _4 \times 10 ^4 \; rad/s^2}= 3.14\;s}\)

(a) 
\(\mathrm{a_t = rd \\ \therefore d = \frac{a_t}{r}= \frac{- 15.0\;m/s^2 }{0.300\;m}-50.0\;rad/s^2 }\)

(b)
\(\mathrm{v = rw \; \therefore w = \frac{v}{r}\\ At\; t= 4.00\;s, w = \frac{45.0\;m/s}{0.300\;m}= 150\; rad/s \\} \)

\(\begin {align} \mathrm{w = w_o + dt \; \therefore w_o} & = \mathrm {w - dt}\\ & = \mathrm{150 \;rad/s - \bigg(-50.0 \frac{rad}{s^2} \bigg)(4.00\;s)}\\ &= \mathrm{350\; rad/s} \end {align}\)

(c)

\(\begin {align} \mathrm{\theta} & = \mathrm{w_ot +\frac{1}{2} dt^2}\\ & = \mathrm{\bigg( 350\; \frac{rad}{s} \bigg)(4.00 \; s)+\frac{1}{2} \bigg( -50.0 \;\frac{rad}{s^2} \bigg)(4.00\;s)^2} \\ & = \mathrm{1.00 \times 10^3 \; rad} \end {align}\)

(a) \(\mathrm{I = \sum _i \;m_i\; r_i {^2}}\)

For each sphere, 

\(\begin {align} \mathrm{r^2} & = \mathrm{[(0.190)^2 +(0.190)^2]m^2} \\ & = \mathrm{0.0722\;m^2} \end {align}\)

\(\mathrm{\therefore\; I = 4 (0.250 \; kg)(0.0722\;m^2)= 0.0722\; kg \cdot m^2}\)

(b)

For each sphere, \(\mathrm{r = 0.190\;m}\)

\(\mathrm{\therefore\; I = 4 (0.250\; kg)(0.190\;m)^2 = 0.0361 \; kg \cdot m^2}\)

\(\mathrm{\omega = \omega_o + \alpha t \\ 2.15 \;rad/s = 4.25 \;rad/s + \alpha (6.5\; s)}\)

\(\mathrm{\alpha = \frac{(2.15\; rad \cdot s^{-1} - 4.25 \;rad \cdot s^{-1})} {(6.5 \;s)} = -0.323 \;rad \cdot s^{-2} \\ \tau = I \alpha = (31.5 \;kg \cdot m^2)(-0.323\; rad \cdot s^{-2}) \\ \tau = -10.2 \;N \cdot m}\)

\(\mathrm{v = \omega \;r \therefore \; \omega = \frac{v}{r}= \frac{5.50\;m/s}{0.260\;m}= 21.1_5 \; rad/s}\)

\(\mathrm{\omega = \omega_o + dt \therefore \propto = \frac{\omega-\omega_o}{t}= \frac{(21.1_5)rad/s}{0.150\;s}= 141.0 \; rad/s^2}\)

\(\mathrm{\tau_{NET} = I \propto \\ \therefore T (0.024\;m)= (0.0700 \;kg \cdot m^2)(141.0 \; rad/s^2) \\ \therefore \; T = 411\; N}\)

(a)

\(\begin {align} \mathrm{F_K} & = \mathrm{\mu _K \;N}\\ & = \mathrm{0.750 (13.0\;N)} \\ & = \mathrm{9.75\;N} \end {align}\)

\(\mathrm{\tau _{NET} = I \propto , \; about \; 0 \\ \therefore - F_{K\cdot r} = I \propto \\ \therefore - (9.75\;N)(0.280\;m)= (0.420\; kg \cdot m^2) \propto \\ \Rightarrow \propto = -6.50\; rad/s^2 \\ \omega = \omega_o + \propto t \therefore t = \frac{\omega-\omega_o}{\propto}= \frac{(0-20.0)rad/s}{-6.50\;rad/s^2}= 3.08\;s}\)

(b) Work done:

\(\begin {align} \mathrm{W} &= \mathrm{\Delta K E} \\ & = \mathrm{KE_f - KE_i} \\ & = \mathrm{0 - \frac{1}{2}I w_o{^2}}\\ & = \mathrm{- \frac{1}{2}(0.420 \; kg \cdot m^2)(20.0\; rad/s)^2} \\ & = \mathrm{- 84.0 \; J} \end {align}\)

\(\mathrm{grav.\;P\cdot E\cdot \;at \; top = K \cdot E \cdot \; at \; bottom \\ \therefore M\; g\; y = \frac{1}{2} M\; v^2 + \frac{1}{2}I w^2 \\ Subst\cdot\; I = \frac{2}{5} MR^2 \; and \; w = \frac{v}{r}: \\ \therefore M\;g\;y = \frac{1}{2}Mv^2 + \frac{1}{2}\bigg( \frac{2}{5}MR^2 \bigg) \frac{v^2}{R^2} \\ \therefore g\;y = \frac{1}{2} v^2+\frac{1}{5}v^2 \\ = \frac{7}{10} v^2 \\ \therefore v = \sqrt{\frac{10}{7}g\;y}= \sqrt{\frac{10}{7}(9.80\;m/s^2)(20.0\;m)}= 16.7\;m/s}\)

\(\mathrm{Initial\; grav. \;P.E. \;of\; mass}\)  \(\mathrm{m = final \; K.E. \; of \; m \; + final \; KE \;of\; cylinder }\)

\(\mathrm{\therefore m\;g\;h = \frac{1}{2}m\;v^2+\frac{1}{2}I\omega^2 \quad [1]}\)

For a cylinder, \(\mathrm{I = \frac{1}{2}M\;R^2 \quad [2]\; (Table\; 9-1)}\)

\(\begin {align} \mathrm{speed\;v\; of \; mass \; m} & = \mathrm{speed\; v\; of\; cable } \\ &= \mathrm{speed\; v\; of\; rim\; of\; cylinder} \end {align}\)

\(\mathrm{\therefore v = \omega\; R\; or\; \omega =\frac{v}{R}\quad [3]}\)

\(\mathrm{Subst.\; [2] \; and\; [3] \; into \; [1]: \\ \therefore \;m\;g\;h = \frac{1}{2}m\;v^2 + \frac{1}{2}\bigg( \frac{1}{2} MR^2\bigg)\frac{v^2}{R^2}\\ \therefore \;m\;g\;h = \frac{1}{2}v^2\bigg( m+\frac{1}{2} M\bigg)}\)

Divide both sides by \(\mathrm{m \Rightarrow g\; h = \frac{1}{2}v^2 \bigg( 1+ \frac{M}{2m} \bigg)}\)

\(\mathrm{\therefore\; v = \sqrt {\frac{2\;g\;h}{1+ \frac{M}{2m}}}}\)

From \(\mathrm{[3]}\), \(\mathrm{\omega = \frac{v}{R}= \frac{1}{R}\sqrt{ \frac{2\;g\;h}{1+ \frac{M}{2m}}}}\)

(a)

\(\mathrm{\omega_1 = 0.640 \frac{rev}{s} \times \frac{2\pi \;rad}{1\; rev} = 4.02\; rad/s \quad (4.02_1 \; \frac{rad}{s})}\)

(b) Angular momentum is conserved. 

\(\mathrm{\therefore \; I_2 \omega_2 = I_1 \omega _1 \\ Given \; : I_2 = \frac{2}{3}I_1 \\ \therefore \frac{2}{3} \; I_1 \omega_2 = I_1 \omega _1 \\ \therefore \omega _2 = \frac{3}{2} \; \omega _1 = 6.03\; rad/s}\)

\(\mathrm{\omega_1 = \frac{2.00\;rev}{1.30\;s}= 1.53_8 \; \frac{rev}{s}}\)

Angular momentum is conserved \(\mathrm{\therefore\; I_1 \omega _1 = I_2 \omega _2}\)

\(\mathrm{\therefore \omega_2 = \frac{I_1}{I_2} \omega _1 = \frac{4.60\;kg\cdot m^2}{19.0\; kg \cdot m^2} \times 1.53_8 \frac{rev}{s}= 0.372_5 \; \frac{rev}{s}}\)

\(\mathrm{\therefore \; \# \; of \; rev's \; in \; 1.60 \;s : \; 0.372_5 \frac{rev}{s} \times 1.60\;g = 0.596\;rev}\)

\(\begin {align} \mathrm{Initial: \; I_1} & = \mathrm{400\;kg \cdot m^2 + (19.0\;kg)(2.oo\;m)^2}\\ & = \mathrm{476\; kg \cdot m^2} \\ \mathrm{Final : I_2} & = \mathrm{400\;kg \cdot m^2 + (19.0\;kg)(1.00\;m)^2} \\ & = \mathrm{419\; kg \cdot m^2} \end {align}\)

Angular momentum is conserved \(\mathrm{\therefore I_1 \omega_1 = I_2 \omega_2}\)

\(\mathrm{\therefore \omega _2 = \frac{I_1}{I_2}\omega_1 = \frac{476}{419}(0.500\;rev/s)= 0.568\;rev/s}\)

At top, \(\mathrm{\sum F_y = m\;a_y \Rightarrow T_1 + m\;g = m \frac{v_1{^2}}{r} \quad [1]}\)

At bottom, \(\mathrm{\sum F_y = m\;a_y \Rightarrow T_2 - m\;g = \frac{v_2{^2}}{r}\quad [2]}\)

Energy is conserved

\(\mathrm{\therefore m\;g\;y_1 + \frac{1}{2} m\;v_1{^2}= m\;g\;y_2 + \frac{1}{2}m\;v_2{^2} \\ \therefore v_2{^2}= v_1{^2}+ 2\;g (y_1 - y_2)}\)

But \(\mathrm{y_1 - y_2 = 2r}\) \(\mathrm{\therefore v_2{^2}= v_1{^2}+ 4\;g\;r. \; Subst.\; in \;[2]}\)

\(\mathrm{\therefore T_2 - m\;g = m\frac{v_1{^2}}{r}+ 4\;m\;g \\ \therefore \; T_2 = m\frac{v_1{^2}}{r}+ 5\;m\;g \quad [3]}\)

But, from \(\mathrm{[1],}\)  \(\mathrm{\frac{mv_1{^2}}{r}= T_1+\;m\;g.\; Subst. \; in \; [3]}\)

\(\mathrm{\therefore T_2 = T_1 + \;m\;g+ 5\;m\;g \\ \therefore T_2 = T_1 + 6\;m\;g}\)

(a)

The nornal force \(\mathrm{\overrightarrow N}\) has a horizontal component, \(\mathrm{N \sin \theta}\), which points toward the centre of the circle. Hence, this horizontal component of \(\mathrm{\overrightarrow N}\) constitutes the centripetal force. 

(b)

\(\mathrm{\sum F_x = m\;a_x = m\;a_c \; \therefore N\sin \theta = m\frac{v^2}{r} \quad [1] \\ \sum F_y = m\;a_y = 0\; \therefore N \cos \theta - \;m\;g = 0 \\ \therefore N\cos \theta = \;m\;g \quad[2] \\ [1] \div [2] \Rightarrow \tan \theta = \frac{v^2}{g\;r}\\ v = 100 \frac{km}{h}\times \frac{1h}{3600s}\times \frac{1000m}{1km}= 27.7_8 \;m/s \\ \therefore \tan \theta = \frac{(27.7_8 \;m/s)^2}{(9.80\;m/s^2)(500m)}\\ \Rightarrow \theta = 8.95^\circ}\)

(a)

\(\mathrm{\sum F_y = m\;a_y = 0\\ \therefore \; T \cos 45.0^\circ - m\;g = 0 \; \therefore T = \frac{m\;g}{\cos\; 45.0^\circ} \quad [1]\\ \rightarrow T = 3.33 \times 10^3 \;N \quad (3.32_6 \times 10^3\;N)}\)

(b)

\(\mathrm{\sum F_x = m\;a_x = m\;a_c \\ \therefore T \sin 45.0 ^\circ = m \frac{v^2}{r} \quad [2]}\)

\(\mathrm{[2] \Rightarrow v = \sqrt{\frac{rT \sin 45.0^\circ}{m}}\\ But\; T = \frac{m\;g}{\cos 45.0^\circ} \quad [1]\\ \therefore v = \sqrt{rg\frac{\sin 45.0^\circ}{\cos 45.0^\circ}}= \sqrt{rg \tan45.0^\circ}\\ But\; \tan\; 45.0^\circ = 1 \\ \therefore \underbrace {v = \sqrt{rg} }_\text {independent of mass m}= \sqrt{(9.19_2\;m)(9.80\;m/s^2)}\\ = 9.49\;m/s}\)

\(\mathrm{\therefore}\) upper hinge must prevent this motion

\(\mathrm{\overrightarrow F_{upper}}\) is towards right, as shown. 

\(\mathrm{\sum \tau = 0\; about \; P. \\ \therefore m\;g (1.20\; m)- F_{upper}(1.00\;m)= 0\\ \Rightarrow F_{upper}= 600\;N \quad (599._8\; N)\\ \sum F_x = 0 \therefore F_{upper}+ F_{lower, x}= 0\\ \Rightarrow F_{lower, x}= -599._8\;N \\ \sum F_y = 0 \therefore F_{lower, y}- m\;g = 0\\ \Rightarrow F_{lower,y}= 499._8 \; N}\)

\(\mathrm{\Rightarrow F_{lower}= 781\;N}\\ \theta = 39.8^\circ\)

(a)

\(\mathrm{\sum \tau = 0\; about P.\\ Let \; \ell = length\; of \; strut \\ \therefore F_{pivot} (0)+ T(\ell \cos 75.0^\circ)- (m_s\;g)(\frac{\ell}{2}\cos 45.0^\circ)\\ - (m\ g)(\ell \cos 45.0^\circ)= 0 \\ \therefore m = \frac{T}{g}\frac{\cos 75.0^\circ}{\cos 45.0^\circ}- \frac{m_s}{2}= 697\; kg \quad (697.0\;kg)}\)

(b)

\(\mathrm{\sum F_x = 0 \\ \therefore F_{pivot, x}+ T_x = 0 \\ T_x= -T \cos 30.0^\circ = -1.73_2 \times 10^4 \;N\\ \therefore F_{pivot, x}= + 1.73_2 \times 10^4 \; N\\ \sum F_y = 0\\ \therefore F_{pivot, y}+ T_y - m_s \;g - m\;g = 0 \\ \therefore F_{pivot, y}= (m_s + m)g - T_y \\ T_y = -T \sin 30.0^\circ = -1.00_o \times 10^4 \;N \\ \Rightarrow F_{pivot, y}= 1.78_1 \times 10^4 \;N} \)

\(\mathrm{\Rightarrow F_{pivot}= 2.48 \times 10^4 \;N \\ \theta = 45.8^\circ}\)

(a) FBD for foot:

\(\sum \tau = 0 \; \text{about P.} \\ \therefore \mathrm{F} \bigg( \frac{3\mathrm{L}}{4} \sin 60.0^\circ \bigg) - \mathrm{T} \bigg( \frac{\mathrm{L}}{4} \sin 70.0^\circ\bigg) + \mathrm{F_L} (0) = 0 \\ \therefore \mathrm{T} = \frac{3\mathrm{F}\sin60.0^\circ}{\sin 70.0^\circ} = 2.76 \mathrm{F} \quad (2.76_5 \mathrm{F})\)

(b) FBD of foot:

\(\begin {align} T_x & = T \cos 40.0^\circ \\ & = 2.11_8 \;F \\ T_y & = T \sin 60.0^\circ \\ & = 1.77_8 \; F \end {align}\)

\(\sum F_x = 0 \\ \therefore F_{L, x} + T_x = 0 \Rightarrow F_{L,x} = -2.12 \quad F \\ \sum F_y = 0 \\ \begin {align} \therefore F+F_{L,Y} + T_y = 0 \Rightarrow F_{L,y} & = -F-T_y \\ & = -F-1.77_8\;F \\ &= - 2.78\;F \end {align}\)

(a) FBD for Ladder:

\(\sum \tau = 0\; \text{about P.} \\ PC = 10.0\; \mathrm{m} \\ QC = 6.00\; \mathrm{m} \\ \therefore PQ = 8.00 \; \mathrm{m}\; \text{(Pythagoras)} \\ \emptyset = \tan^{-1} \bigg( \frac{PQ}{QC} \bigg) = 53.1_3{^\circ} \\ PR = 5.00\; \text{m}, \;PB = 7.00\; \text{m},\; PD = QC = 6.00\; \text{m}\\ \therefore \text{about P,} \sum \tau = N_1 (0) +N_2 (PD) - F_f (PQ) - Mg (PE) - mg (PF) = 0 \\ \text{To find} \;N_2, \; \text{use} \; \sum F_y = m\; a_y = 0 \quad \uparrow+y \\ \therefore N_2 - Mg - mg = 0 \\ \therefore N_2 = Mg + mg \quad [1] \\ \therefore \sum \tau = (Mg+mg)PD - F_f (PQ)- Mg (PE) -mg (PF) = 0 \quad [2] \\ \therefore (400+800)(6.00)-F_f(8.00)-4.00 (5.00 \cos 53.1_3 {^\circ})\\ -800(7.00 \cos 53.1_3{^\circ}) =0\\ \Rightarrow F_f = 3.30 \times 10^2 N\)

(b)

\(\begin {align} \text{Max. Friction} \quad F_{max} = \mu_3 \;N_2 & = 0.400 (Mg+mg) \\ &= 0.400 (400+800) \\ &= 480 \;N \end {align}\)

Now, redo \([2],\) replacing \(F_4\) by \(F_{max}\) and the unknown is the new value of \(PF\) (write this as \("PF"\))

\(\therefore (400+800)(6.00)- (480)(8.00)-400 (5.00 \cos 53.1_3 {^\circ})- 800 (''PF'' = 0\\ \Rightarrow \; ''PF'' = 2.70_0 \text{m} \\ \text{But} \; ''PF''= ''PB'' \cos \emptyset \\ \therefore \; ''PB'' = \frac{''PF''}{\cos 53.1_3 {^\circ}}= 4.50\; \text{m} \\ \therefore \; ''BC'' = (10.0 - 4.50) \text{m} = 5.5 \;\text{m}\)

(a)

\(\tau _{net} = \tau \propto, \; \text{where} \; \tau _{net} = 20.0 \; N \cdot \text{m} \\ \text {Speeding up}\; \omega = \omega_o + \propto t \\ \therefore\; \propto = \frac{\omega - \omega_o}{t}= \frac{100 \frac{\text{rev}}{\text{min}}\times \frac{1 \; \text{min}}{60\text{s}}\times \frac{2\pi \text{rad}}{1\text{rev}}}{10.0 \text{s}} = 1.04_7 \; \text{rad/s}^2 \\ \therefore \tau _{net} = \tau \propto \Rightarrow 20.0 = I (1.04_7) \therefore I = 19.1 \; \text{kg} \cdot \text{m}^2 \quad \mathrm{(19.1_0 \; kg\cdot m^2)}\)

(b)

\(\text{Slowing down:} \; \omega_s = \omega _{os} + \propto_st_s \\ \therefore \; \propto_2 = \frac{\omega_s - \omega_{os}}{t_s} = \frac{-100\frac{\text{rev}}{\text min}\times \frac{1 \text min}{60\text s}\times\frac{2\pi \text rad}{1 \; \text {rev}}}{100 \text s}= -0.104_7\; \text {rad/s}^2 \\ \tau_{net, s} = I \propto_s \; \therefore \tau_{friction}= (19.10)(-0.104_7) = -2.00 \; N \cdot \text m \\ \therefore | \tau _{friction} | = 2.00 N \cdot \text m\)

(c)

\(\begin {align} \text {Speeding up:} \; \theta & = \omega_ot+\frac{1}{2} \propto t^2 \\ & = 0+ \frac{1}{2} (1.04_7)(10.0)^2 \\ &= 52.3_5\; \text{rad} \end {align}\)

\(\begin {align} \text{Slowing down:} \; \theta_s &= \omega_{os}t_s + \frac{1}{2} \propto _s t_s {^2} \\ & = (10.4_7)(100)+ \frac{1}{2}(-0.104_7)(100)^2 \\ &= 523._5 \; \text{rad} \end {align}\)

\(\therefore \; \text{total angle} = 575._9 \; \text{rad} \times \frac{1\; \text{rev}}{2 \pi \; \text{rad}} = 91.7 \; \text{rev}\)

FBD of a yo-yo:

\(\sum F_y = m\; a_y \; \downarrow + y \\ \therefore 2 \;Mg - T = 2M \;a \quad [1] \\ \text{Also, } \;\sum \tau = I \propto, \text{about centre of yo-yo}\\ \therefore (2Mg)(0) + T \cdot b = I \propto \\ \begin {align} \text{Now, }\; I & = \frac{1}{2}MR^2 + \frac{1}{2}MR^2 \text{(Table 9-1)}\\ & = MR^2 \\ \therefore \; T \cdot b & = MR^2 \propto \quad [2] \end {align}\)

The yo-yo is essentially rolling down the string. 

\(\begin {align} \therefore \; \text{downward velocity} \; v &= \omega r, \text{where} \; r = b \\ \therefore \; v & = \omega b \\ \therefore \frac{dv}{dt} & = \frac{dw}{dt}b \\ \therefore \; a & = \propto b \\ \therefore \; \propto & = \frac{a}{b} \cdot \text{Subst. in } [2] \\ \therefore \; T \cdot b& = MR^2 \frac{a}{b} \\ \therefore \; T & = MR^2 \frac{a}{b^2} \quad [3] \; \text{Subst. in}\; [1] \\ \therefore \; 2Mg - MR^2 \frac{a}{b^2} & = 2 \; Ma \\ \div 2M \Rightarrow \quad g - \frac{R^2}{2b^2} a & = a \\ \therefore\; g & = a \bigg( 1+ \frac{R^2}{2b^2} \bigg) \\ \therefore \; a & = \frac{g}{1+ \frac{R^2}{2b^2}} \end {align}\)

\(\text{Then, in [3]}: T = \frac{MR^2}{b^2} \frac{g}{1+ \frac{R^2}{2b^2}}\)

Energy is conserved.

\(\therefore \; \text {Grav. P.E. of B at Beginning } = KE_A + KE_b+KE _{Pulley} + E_{Thermal} \\ \therefore m_B \; g \; h = \frac{1}{2}m_Av_A {^2}+\frac{1}{2}m_Bv_B{^2}+ \frac{1}{2}I \omega^2 + F_K \Delta r_B \\ \text{But} \; v_A = v_b. \quad \therefore \; \text{write} \; v_A = v_B= v \\ \text{Also, speed of rim of pulley} \; = v, \text{and} \; v= \omega \; R \therefore \omega = \frac{v}{R} \\ \begin {align} \therefore \; m_B\; g\; h &= \frac{1}{2} m_Av^2 + \frac{1}{2}m_B v^2 +\frac{1}{2}I \frac{v^2}{R^2} + F_K \Delta r_A \\ &= \frac{v^2}{2}\bigg( m_A + m_B + \frac{I}{r^2} \bigg) + F_K \Delta r_A \end {align} \)

\(\begin {align} \text{Now, } \Delta r_A = h, \; \text{and} F_K &= \mu_K N_A \\ &= \mu _K m_A g\; (\because \sum F_{AY}= m\; a_{AY}= 0) \end {align} \\ \therefore \; m_B\; g\; h = \frac{v^2}{2}\bigg( m_A+ m_B + \frac{I}{r^2} \bigg) + \mu_K m_A \; g\; h \\ \therefore \; 2 \; g\; h (m_B - \mu _K m_A) = v^2 \bigg( m_A + m_B + \frac{I}{r^2} \bigg) \\ \therefore \; v = \sqrt{\frac{2\; g\; h (m_B - \mu_K m_A)}{m_A +m_B + \frac{I}{r^2}}}\)

Angular momentum is conserved. 

\(\therefore \; I_1 \omega _1 = I_2 \omega_2 \\ I_1 = \frac{1}{2}MR^2 \text{(turntable, from table 9-1)}\\ \text{and} \; I_2 = \frac{1}{2}MR^2 + mR^2 = \bigg( \frac{M}{2}+ m \bigg) R^2\)

\(\begin {align} \omega _1 = 33\frac{1}{3} \frac{\text{rev}}{\text{min}}\times \frac{2\pi \; \text{rad}}{1\; \text{rev}} \times \frac{1 \; \text{min}}{60\; \text{s}} &= 3.49_1 \; \text{rad/s} \\ \therefore \; \omega _2 = \frac{I_1}{I_2} \omega_1 = \frac{\frac{1}{2} M \require{cancel} \cancel {R^2}}{\bigg( \frac{M}{2} + m\bigg) \require{cancel} \cancel {R^2}} \omega_1 & = \frac{0.100}{0.200} 3.49_1 \\ &= 1.74_5 \; \text{rad/s} \end {align}\)

\(\begin {align} \Delta KE & = \frac{1}{2}I _2 \omega _2{^2} - \frac{1}{2}I_1 \omega_1{^2} \\ &= \frac{1}{2}\bigg[ \bigg( \frac{M}{2}+ m \bigg) R^2 \omega_2{^2} - \bigg( \frac{1}{2} MR^2\bigg) \omega_1{^2} \bigg] \\ &= \frac{1}{2} \bigg[ (0.200)(0.105)^2(1.74_5)^2 - (0.100)(0.105)^2(3.49_1)^2 \bigg] \\ & = - 3.36 \times 10^{-3} J \end {align}\)