DC Circuits - Part A
Schematic Diagrams
This section lists the main components of d.c. (direct current) circuits that you will encounter in your physics classes.
| Symbol | Description |
|---|---|
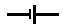 |
This is a source of emf (electromotive force), with a voltage of \(\varepsilon\) , measured in units of volts, \(V.\) The most common source you will see will be a battery. |
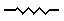 |
This is a resistance, measured in units ohms ohms,\(\Omega\) . Most often it will be a resistor. However, wires connecting parts of a circuit are really not resistance-free. We can model this real-life case by putting a 'resistor' in the circuit which has the same resistance as the wires would have. Thus the wires can still be considered resistance-free since their resistance is represented by an additional resistor. |
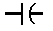 |
This is a capacitor, with capacitance \(C\) measured in units of farads, \(F.\) The perfect capacitor will have no resistance (or inductance; see next), and we will assume that this symbol represents such an ideal capacitor. If a capacitor is not ideal, that is, it has some resistance (or inductance) associated with it, then we can model this by putting a 'resistor' (or inductor) in parallel with the capacitor. This resistor (or inductor) will have the same resistance (or inductance) as the non-ideal capacitor. |
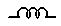 |
This is an inductor, with inductance \(L,\) measured in units of henrys, \(H.\) To model a non-ideal inductor in a circuit (an inductor with an associated resistance or capacitance) we can put a resistor in series or a capacitor in parallel with the inductor. Giving these the same values as the inductor will represent an imperfect inductor. |
Ohm's Law
- Ohm's Law deals with the relationship between voltage and current in an ideal conductor. This relationship states that:
The potential difference (voltage) across an ideal conductor is proportional to the current through it.
The constant of proportionality is called the "resistance", \(R.\)
Ohm's Law is given by:
\(V = I R\)
where \(V\) is the potential difference between two points which include a resistance \(R.\) \(I\) is the current flowing through the resistance. For biological work, it is often preferable to use the conductance, \(g = 1/R\); In this form Ohm's Law is:
\(I = g V\)
- Material that obeys Ohm's Law is called "ohmic" or "linear" because the potential difference across it varies linearly with the current.
- Ohm's Law can be used to solve simple circuits. A complete circuit is one which is a closed loop. It contains at least one source of voltage (thus providing an increase of potential energy), and at least one potential drop i.e., a place where potential energy decreases. The sum of the voltages around a complete circuit is zero.
- An increase of potential energy in a circuit causes a charge to move from a lower to a higher potential (ie. voltage). Note the difference between potential energy and potential.
Because of the electrostatic force, which tries to move a positive charge from a higher to a lower potential, there must be another 'force' to move charge from a lower potential to a higher inside the battery. This so-called force is called the electromotive force, or emf. The SI unit for the emf is a volt (and thus this is not really a force, despite its name). We will use a script E, the symbol \(\varepsilon\), to represent the emf.
A decrease of potential energy can occur by various means. For example, heat lost in a circuit due to some electrical resistance could be one source of energy drop.
Because energy is conserved, the potential difference across an emf must be equal to the potential difference across the rest of the circuit. That is, Ohm's Law will be satisfied:
\(\varepsilon = I R\)
Resistors in Series
Resistors can be connected in series; that is, the current flows through them one after another. The circuit in Figure 1 shows three resistors connected in series, and the direction of current is indicated by the arrow.
Note that since there is only one path for the current to travel, the current through each of the resistors is the same.
- \(I = I_1 = I_2 = I_3\)
Also, the voltage drops across the resistors must add up to the total voltage supplied by the battery: - \(V_\mathrm{total} = V_1+V_2+V_3\)
Since \(V = I R\), then - \(V_\mathrm{total} = I_1 R_1+I_2R_2+I_3R_3\)
But Ohm's Law must also be satisfied for the complete circuit: - \(V_\mathrm{total} = I \cdot R_\mathrm{equivalent}\)
Setting equations 3. and 4. equal, we get: - \(I\cdot R_\mathrm{equivalent} = I_1 \cdot R_1+ I_2 \cdot R_2 +I_3 \cdot R_3\)
We know what the current through each resistor (from equation 1.) is just \(I\). - \(I \cdot R _\mathrm{equivalent} = I (R_1 + R_2 +R_3)\)
So the currents cancel on both sides, and we arrive at an expression for equivalent resistance for resistors connected in series. - \(R_\mathrm{equivalent} = R_1 +R_2 +R_3\)
In general, the equivalent resistance of resistors connected in series is the sum of their resistances. That is, - \(R_\mathrm{equivalent} = \sum R_i\)
This can also be written in terms of conductances, since conductance is just the reciprocal of resistance: - \(\frac{1}{g} = \sum \frac{1}{g_1}\)
Resistors in Parallel
Resistors can be connected such that they branch out from a single point (known as a node), and join up again somewhere else in the ciruit. This is known as a parallel connection. Each of the three resistors in Figure 1 is another path for current to travel between points \(A\) and \(B.\)
Note that the node does not have to physically be a single point; as long as the current has several alternate paths to follow, then that part of the circuit is considered to be parallel. Figures 1 and 2 are identical circuits, but with different appearances.
At \(A\) the potential must be the same for each resistor. Similarly, at \(B\) the potential must also be the same for each resistor. So, between points \(A\) and \(B,\) the potential difference is the same. That is, each of the three resistors in the parallel circuit must have the same voltage.
- \(V_1 = V_2 = V_3 = V\)
Also, the current splits as it travels from \(A\) to \(B.\) So, the sum of the currents through the three branches is the same as the current at \(A\) and at \(B\) (where the currents from the branch reunite).
- \(I = I_1+I_2+I_3\)
By Ohm's Law, equation 2. is equivalent to:
- \(\frac{V}{R_\mathrm{equivalent}} = \frac{V_1}{R_1}+\frac {V_2}{R_2}+\frac {V_3}{R_3}\)
By equation 1., we see that all the voltages are equal. So the V's cancel out, and we are left with
- \(\frac{1}{R_\mathrm{equivalent}} = \frac{1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}\)
This result can be generalized to any number of resistors connected in parallel.
- \(\frac {1}{R_\mathrm{equivalent}} = \sum \frac {1}{R_i}\)
Since resistance is the reciprocal of conductance, equation [5] can be expressed in terms of conductances.
- \(g_\mathrm{equivalent} = \sum g_i\)