Dimensional Analysis Tutorial
When doing physics problems, you'll often be required to determine the numerical value and the units of a variable in an equation. The numerical value usually isn't too difficult to get, but for a novice, the same can't be said for the units. This self-instruction unit deals with dimensional analysis, which is a useful method for determining the units of a variable in an equation. Another use of dimensional analysis is in checking the correctness of an equation which you have derived after some algebraic manipulation. Even a minor error in algebra can be detected because it will often result in an equation which is dimensionally incorrect.
Objectives
- Given the definition of a physical quantity, or an equation involving a physical quantity, you will be able to determine the dimensions and SI units of the quantity.
- Given an equation, you will be able to determine if the equation is dimensionally correct or incorrect.
Physical Quantities
Most physical quantities can be expressed in terms of combinations of five basic dimensions. These are mass (\(M\)), length (\(L\)), time (\(T\)), electrical current (\(I \)), and temperature, represented by the Greek letter theta (\(\theta\)). These five dimensions have been chosen as being basic because they are easy to measure in experiments. Dimensions aren't the same as units. For example, the physical quantity, speed, may be measured in units of metres per second, miles per hour etc.; but regardless of the units used, speed is always a length divided a time, so we say that the dimensions of speed are length divided by time, or simply \(L/T\). Similarly, the dimensions of area are \(L^2\) since area can always be calculated as a length times a length. For example, although the area of a circle is conventionally written as \(\pi r^2\), we could write it as \(\pi r\) (which is a length) × \(r\) (another length).
Now try Quiz 1
Dimensions of Physical Quantities
Now that you can determine the dimensions of physical quantities, it'll be useful to write the SI units for the quantities. SI stands for International System (Système Internationale). The SI unit for mass is the kilogram, for length the metre, for time the second, for current the ampere, and for temperature the kelvin. Notice that kelvin is abbreviated as just \(K \). The degree symbol, °, and the word "degree" are not used with kelvin.
As a quick example, let's look at speed, which has dimensions of length divided by time or \(L/T\). Its SI units are then metres divided by seconds, represented as \(m/s\) or \(m\cdot s^{-1}\).
Now try Quiz 2
SI Units
Some combinations of SI units are given special names. For example, the unit of energy, \(kg\cdot m^2 /s^2\) , is given the special name joule, which is abbreviated as \(J\). Study the information presented below.
| Physical Quantity | Unit | Mathematical Expression |
|---|---|---|
| energy | joule \((J)\) | \(kg\cdot m^2/s^2\) |
| force | newton \((N)\) | \(kg\cdot m/s^2\) |
| frequency | hertz \((Hz)\) | \((cycles)\cdot s^{-1}\) |
| power | watt \((W)\) | \(J/s = kg\cdot m^2/s^3\) |
| charge | coulomb \((C)\) | \(A\cdot s\) |
You might be wondering when to write joule, \(J\), or \(kg\cdot m^2 /s^2\) as the energy unit. The SI convention is that if there is no number in front of the unit, then the unit is written as a full word. For example, you would write "energy is expressed in joules," with "joules" written out in full, since there is no number associated with it in the sentence. If there is a number, then "\(J\)" ( or less commonly, "\(kg\cdot m^2 /s^2\)") is used. Thus, you would write "the energy is 6.4 \(J\)".
Now try Quiz 3
Dimensionless Quantities
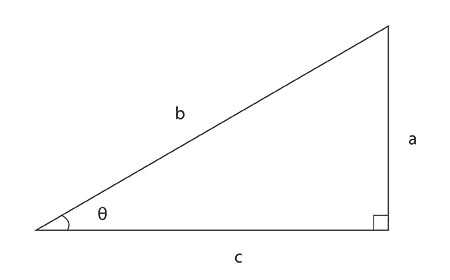
\(\sin\theta=\frac ab\) so,
\(\sin\theta\) has dimensions of \(\frac LL = 1\)
\(\therefore \sin\theta\) is dimensionless
Some quantities have no dimensions. For example, the sine of an angle is defined as the ratio of the lengths of two particular sides of a triangle. Thus, the dimensions of the sine are L/L, or 1. Therefore, the sine function is said to be "dimensionless". There are many other examples of "dimensionless" quantities listed in the following table.
- all trigonometric functions
- exponential functions
- logarithms
- angles (but notice the discussion in the next paragraph)
- quantities which are simply counted, such as the number of people in the room
- plain old numbers (like 2, \(\pi\), etc.)
Notice that some quantities which are "dimensionless" have units. For example, angles can be measured in units of radians or degrees, but angles are "dimensionless". Another familiar example is a frequency unit, (cycles) per second. The second, of course, is a time unit but the cycles are "dimensionless". That's the reason for cycles being written in parentheses above. Take a few moments and learn the "dimensionless" quantities above.
Now try Quiz 4
Special Cases
We've now done all the basics so let's get into some fine points. There are two special cases of quantities which are "dimensionless". First, the argument of a trigonometric function, and second, the exponent in any exponential function. The argument of a trig function is an angle, of course, so it's "dimensionless"; and an exponent of an exponential function is the same thing as a logarithm so it's "dimensionless". These facts often are useful in helping to determine the dimensions of a quantity.
For example, if we're given that \(y = e^{kt}\), where \(t\) is the time, we can state that \(k\) must have dimensions of \(time^{-1}\) in order that the exponent be "dimensionless".
Now try Quiz 5
Common Notation
A common notation, which means "the dimensions of a quantity", is simply the quantity written inside square brackets [ ]; thus, [area] = \(L^2\).
Now try Quiz 6
Dimensionally Correct
In an algebraic expression, all terms which are added or subtracted must have the same dimensions. This implies that each term on the left-hand side of an equation must have the same dimensions as each term on the right-hand side. For example, in the equation \(a = bc + (1/2)xy\), "\(a\)" must have the same dimensions as the product "\(bc\)", and the product "\((1/2)xy\)" must also have the same dimensions as "\(a\)" or "\(bc\)". Remember that the "\(1/2\)" in "\((1/2)xy\)" is just a plain old number and so it has no dimensions.
An equation in which each term has the same dimensions is said to be dimensionally correct. All equations used in any science should be dimensionally correct. The only time you'll encounter one which isn't is if there is an error in the equation. So dimensional analysis is a valuable tool in helping you to detect an equation in which you made an error in algebra, for example. Let's try this out on some equations.
Now try Quiz 7
Sample Question
We're just about finished now. Let's do a sample question. This is a typical question which is fairly difficult. We're given an equation (shown below) involving force, radius, length, speed and distance, and are asked for the dimensions and SI units of eta, \(\eta \), which is viscosity.
\(F = -2\pi rl \frac{v}{R} \eta\)
- \(F\) is force
- \(r\) is radius
- \(l\) is length
- \(v\) is speed
- \(R\) is distance
First, we rearrange the equation to solve for \(\eta\):
\(\eta = \frac{-FR}{2 \pi rlv}\)
Then we convert it to an equation involving dimensions:
\([ \eta ] = \frac{[-1] \cdot[F] \cdot [R]}{[2] \cdot[\pi] \cdot [r] \cdot [l] \cdot [v]}\)
Now try the Dimensional Analysis post-test
If you can do these questions, you're in good shape!