Turning right to go left
Most of us learned how to ride a bike when we were kids, but did you actually learn ‘how’ you ride a bike? If you think about what you do, it might not be immediately obvious, but if I told you to turn right which way would you turn the handlebars? If you’re not on the bike, you might imagine you just turn the handlebars right to go right, but it’s actually the opposite. To turn right, you must first turn left. This process is called counter-steering and is essential to riding bicycles and any other two-wheeled vehicle.
We all learn to do this instinctively through trial and error, but never thought about why we needed to do it. It comes down to physics. When you turn the front wheel right, the rest of the bike follows suit, but you don’t. You are essentially steering the bike out from under you and are now leaning left. The only way to not fall over is to then turn the wheels left and now you’ve turned left instead of right.
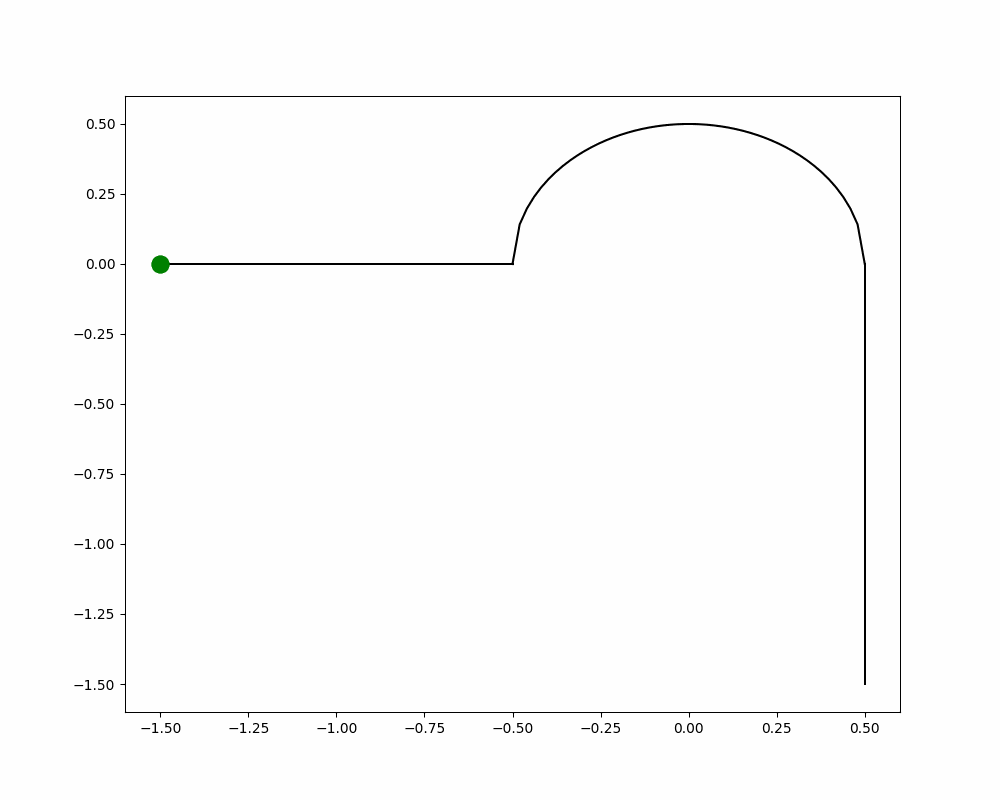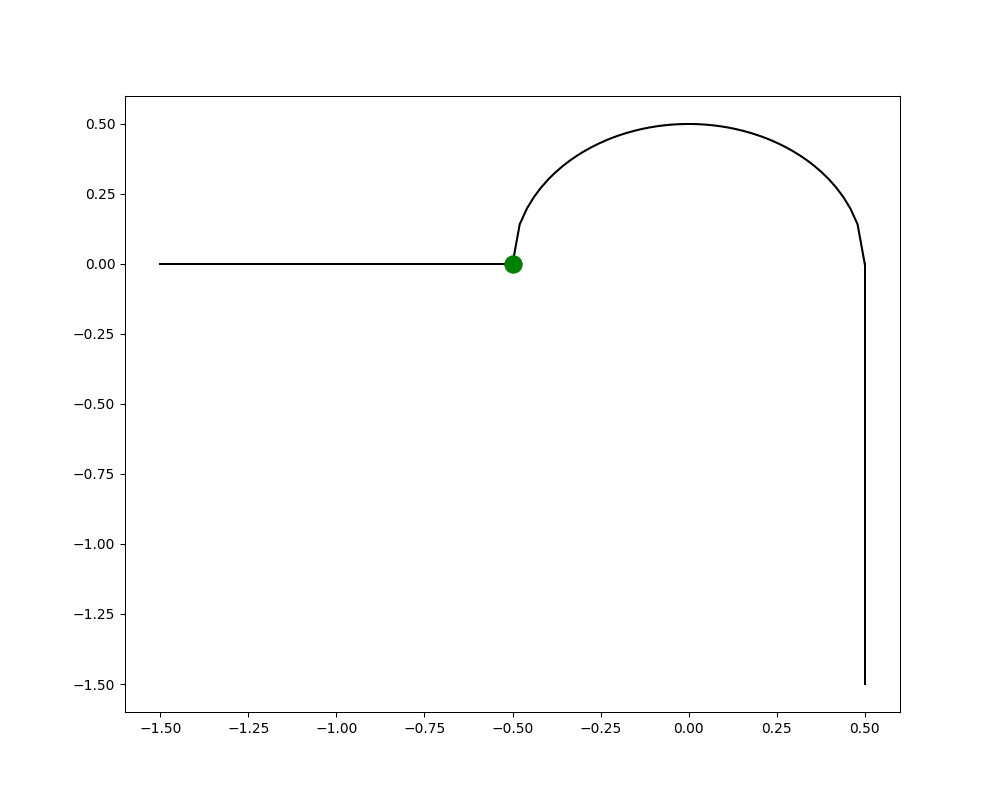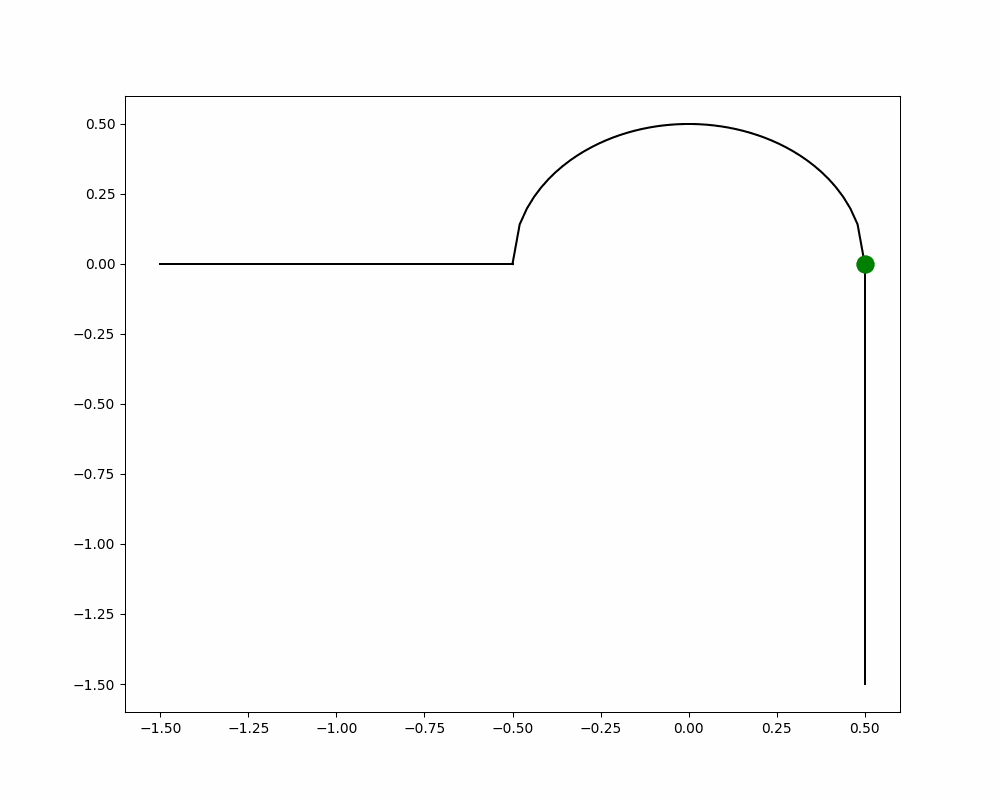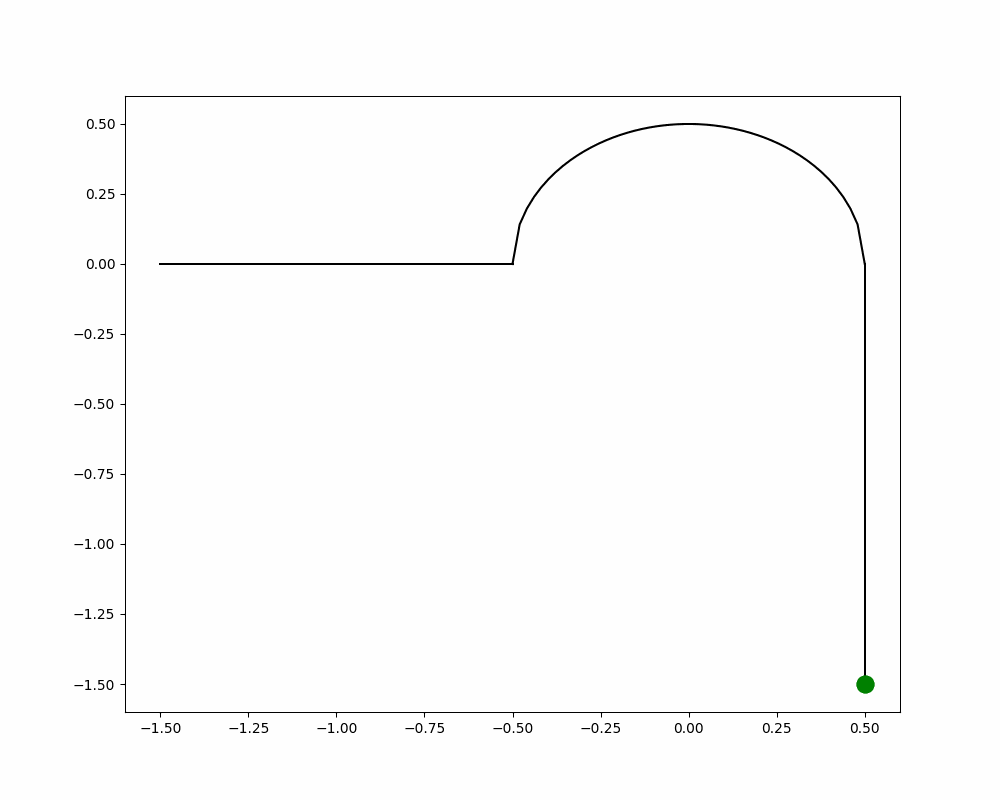
Figure 1a & 1b: Animation constructed using Python of top-down handlebar positioning, corresponding to the position of the bike on its path.
Why does this happen? When you steer the handlebar in one direction, the bike leans the opposite direction (see Fig. 1) due to something called the centrifugal force [1]. To understand this, imagine you’re sitting in a car going straight and coming up to a left turn. When the car starts to turn left, you feel that pull to the right and counter it by leaning left. That force pulling you to the right is the centrifugal force and has the same effect when you turn on a bike. The bike goes left but you go right. This creates a lean which only gets bigger since gravity wants you to eat dirt.
Since the bike is no longer upright, the ground exerts a force on the bike, pushing it in the direction of the lean. This is explained with Newton’s 3rd Law, which says that every force has an equal and opposite reaction force. Put simply, think about the chair you’re probably sitting in to read this. You aren’t falling through it, and that's because the chair is exerting a force on you, equal (in magnitude and opposite in direction) to the force of gravity pulling you into it. This principle holds for every physical interaction.
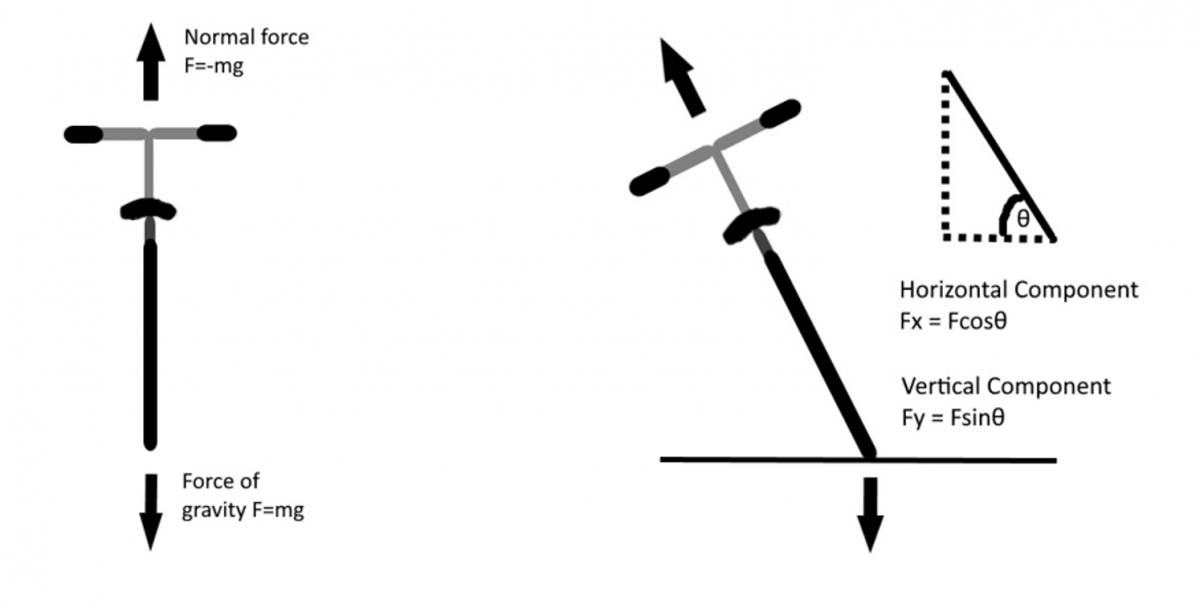
Since the bike is leaning, this reaction force isn’t pushing it straight up, it is instead being pushed in the direction of the lean, further increasing the angle of the lean (see Fig. 2). This is essential to completing a turn and the sharper a turn you want to make, the greater the lean that is required.
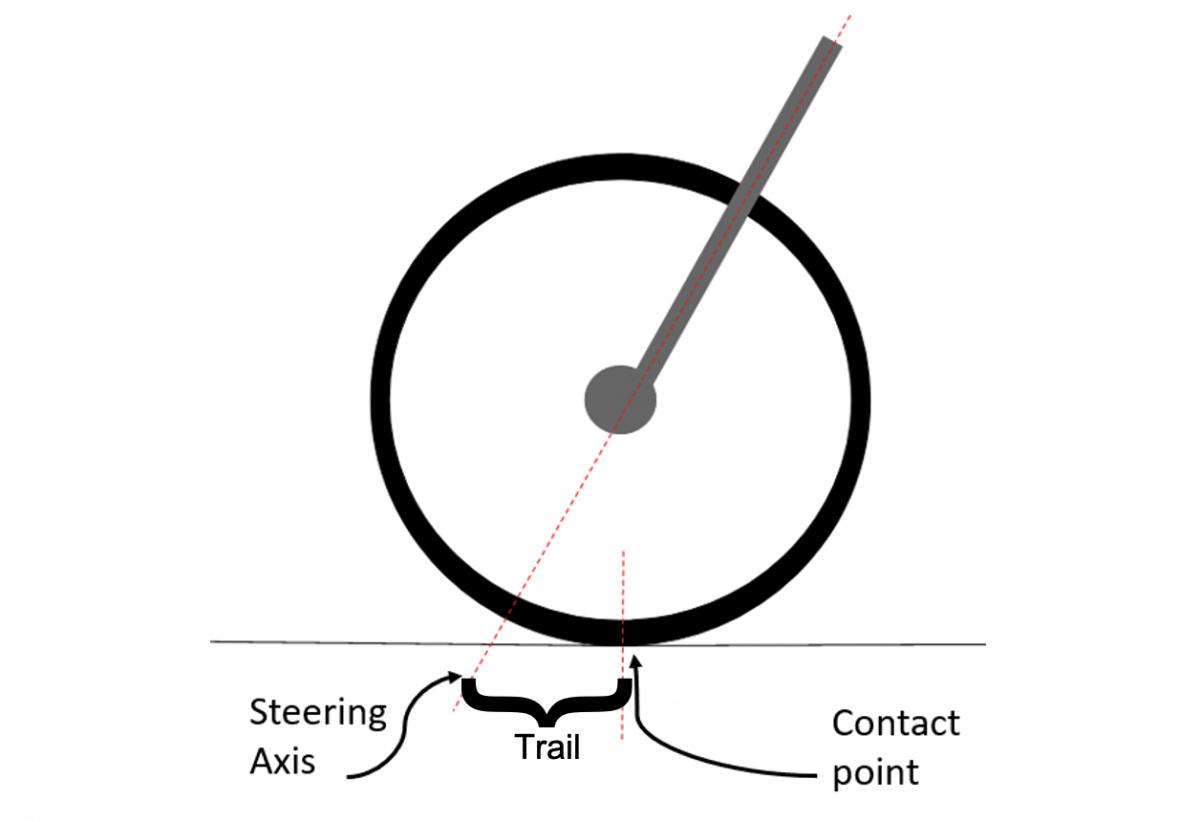
Once a lean has been initiated, by design of the bike, the wheel will begin turning back to the direction of the lean. This happens because the steering axis is on an angle instead of pointing straight down, making it intersect the ground in front of where the wheel actually touches the ground. This means that any lean causes the ground to exert a force on the wheel which will steer it in the direction of that lean [1]. This concept, known as ‘trail’, is considered to be the single largest contributing factor to the stability of a bicycle [2], see Fig. 3.
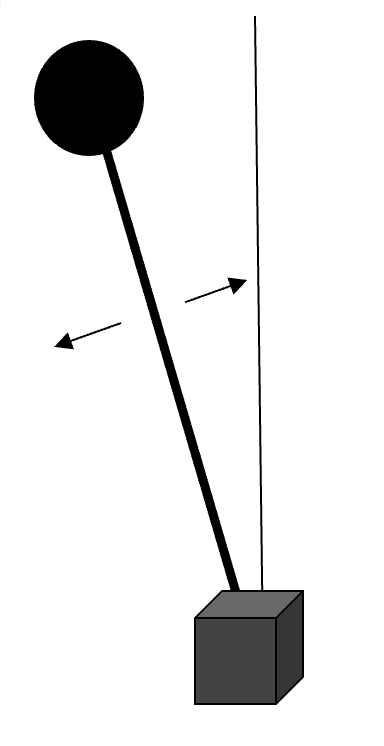
To help understand what's going on, let’s think of a similar situation: imagine an inverted pendulum (see Fig. 4), which you can envision as an upside down grandfather clock, a long object swaying back and forth but fixed at the bottom instead of the top. If you’ve ever tried to balance a ruler or even a broom stick on your hand, you’ve essentially created an inverted pendulum. You would be constantly making minor adjustments to your hand to keep the broom upright. If you wanted to move while balancing it, you would do something similar to what you do with the bike. You pull your hand back to create a forward lean and then you walk with the broom leaning forward. You first have to pull back to move forward; sound familiar?
Riding a bike is something we all take for granted, but it turns out that this machine we believe to be fairly simple and straightforward is actually quite complex when you think about it. Bikes have been around for over 200 years and their mechanisms are still being researched today, which goes to show how ahead of their time they were.
References
- Fajans, J. “Steering in Bicycles and Motorcycles.” American Journal of Physics, vol. 68, no. 7, 2000, pp. 654–59, https://doi.org/10.1119/1.19504.
- Lowell, J., and H. D. McKell. “The Stability of Bicycles.” American Journal of Physics, vol. 50, no. 12, 1982, pp. 1106–12, https://doi.org/10.1119/1.12893.
Christopher Faeth, an undergraduate student at the University of Guelph, produced this article in the context of the 3rd-year course IPS3000 on Science Communication in the Fall 2022 semester (course instructor: Alex Gezerlis, TA: Carley Miki).