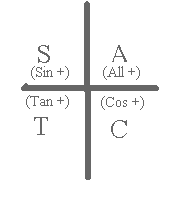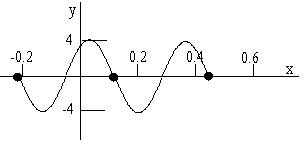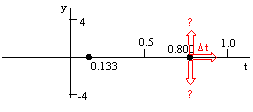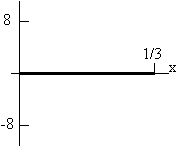Study Guide 1 - Standing and Travelling Waves
Evaluate each of the following:
- Evaluate \(\sin(218^\circ).\)
Note that the argument is in degrees. Now use your calculator.
\(-0.617\)
- Evaluate \(\tan(-48.6^\circ).\)
Note that the argument is in degrees. Now use your calculator.
\(-1.13\)
- Evaluate \(\cos (2.12).\)
In what units is the argument of the cosine?
The argument of the sine function has units of radians, which must be converted to degrees by multiplying by \(\frac{180^\circ}{\pi~\text{rad}}\) to give \(121.47^\circ\)
\(-0.522\) - Evaluate \(\sin (1.78).\)
In what units is the argument of the sine?
The argument of the sine function has units of radians, which must be converted to degrees by multiplying by \(\frac{180^\circ}{\pi~\text{rad}}\) to give \(102^\circ\)
\(0.978\) - Evaluate \(\sin (0.0483).\)
In what units is the argument of the sine?
The argument of the sine function has units of radians, which must be converted to degrees by multiplying by \(\frac{180^\circ}{\pi~\text{rad}}\)
\(0.0483\)Notice that the sine and the angle in radians are equal for small angles, so if you had recognized this at the beginning then the answer could be written down without any calculation. This is known as the small angle approximation.
- Evaluate \(\mathrm {\sin^{-1} (0.687)}\).
Note that the inverse sine \(\sin^{-1}\) means "the angle whose sin is--". The inverse sine is also known as the arcsine, and can be alternatively written as \(\mathrm {\arcsin (0.687)}\) or \(\mathrm {asin(0.687)}\).
Now use your calculator to do the inverse sine operation, but be careful as there are 2 answers!
\(43.4^\circ\) or using the CAST rule \(\mathrm {180 - 43.4 = 136.6^\circ}\). Note that we have 3 significant digits in the first answer, while the second has 4 because of addition/subtraction rules for significant digits.
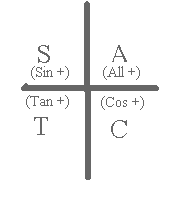
- Evaluate \(\mathrm {\cos^{-1}(2.68)}\).
Watch! There is a trick here.
Can a sine or cosine ever be greater than 1?
No! So there is no possible answer.
- If \(\mathrm {\sin(2\gamma - 2) = 0.444}\), what is \(\gamma\) ?
Watch! There is a trick here.
Let \(\mathrm {2\gamma -2 = \theta}\)
Then \(\sin \theta = 0.444\)Now find \(\theta\):
\(\mathrm {\theta = 26.4^\circ or\; 0.460 \;rad}\)
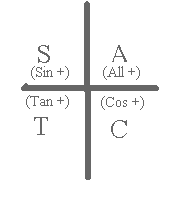
Using the CAST rule \(\theta\) also equals \(\mathrm {180 - 26.4 =153.6^\circ\; or \;2.68\; rad.}\)
Now we see that the quantity \(2\gamma -2\) has two solutions. Do we use the degree or the radian answers?We must use the radian value since the 2 in \(2\gamma -2\) is also in radians.
Solution 1
\(\mathrm {2\gamma - 2 = 0.460\;rad}\)
\(\mathrm {\gamma = 1.23 \;rad\; or \;70.5^\circ}\)Solution 2
\(\mathrm {2\gamma - 2 = 2.68\; rad}\)
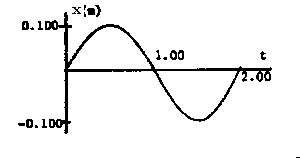
\(\mathrm {\gamma = 2.34\;rad \;or \;134^\circ}\) - Sketch a graph of the equation
\(x=A \sin \biggl(\frac{2 \pi t}{T}\biggr)\)
when the amplitude is 0.100 m and the period is 2.0 s.
This is a positive sine curve with a repeat distance of 2.0 s (the period is 2.0 s) and an amplitude of 0.1 m. Therefore,
\( x=(0.1\; \mathrm{m}) \sin [(\pi\; \mathrm{s^{-1}}) t] \).
-
A wave (SI units) has the equation \(y = 4 \sin (3\pi t - 6\pi x)\)
(a) Is the wave travelling in the \(+x\)- or \(- x\)-direction?
(a) If the time is increased by a small amount, say \(\Delta t\), does \(x\) have to increase by a small amount \(\Delta x\) or decrease to keep \(y\) constant?
Answer
\(\Delta x\) must increase so that \([3\pi (t+\Delta t) - 6\pi (x+\Delta x)]\) is unchanged, i.e., the wave moves in the \(+x\)-direction.
(b) What are the: amplitude, period, wavelength,wave-vector, frequency, angular frequency (all with SI units)?
(b) Compare with the standard form
\(y = A \sin (\omega t - kx)\)
where the angular frequency is defined as
\(\omega = 2\pi f = \frac{2\pi}{T}\)
and the wave vector is defined as
\(k = \frac{2\pi}{\lambda}\).
Answer
Amplitude: \(A = 4 \; \mathrm{m}\)
Wave vector: \( k = 6 \pi \; \mathrm{m}^{-1}= \frac{2 \pi}{\lambda}\)Therefore Wavelength: \(\lambda = 1/3\; \mathrm{m}\)
Angular frequency: \(\omega = 3\pi \; \mathrm {rad/s}\)
Frequency: \(f = \frac{\omega}{2\pi} = 3/2 \;\mathrm {Hz}\)
Period: \(T = 1/f = 2/3 \; \mathrm {s}\)
(c) Sketch the graph of this wave at \(t = 0.900 \; \mathrm{s}\).
(c)
\(y = 4 \sin [(3\pi \mathrm{s}^{-1})( 0.900 \; \mathrm{s}) - (6 \pi \; \mathrm{m}^{-1}) x]\)
Find the places where \(y = 0\), i.e.,
\(y = 0 \; \mathrm{when} \; \sin [(3\pi \; \mathrm{s}^{-1})( 0.900 \; \mathrm{s}) - (6 \pi \; \mathrm{m}^{-1}) x] = 0\).
This requires that
\( 2.7\pi - (6 \pi \; \mathrm{m}^{-1}) x = 0\)
\(\therefore x = 2.7/6 = 0.450 \; \mathrm{m}\)
Of course \(y\) is also 0 at every wavelength multiple (1/3 m see part b, above) on either side of this point, i.e.,
\(0.450 \; \mathrm{m} - 0.333 \; \mathrm{m} = 0.117 \; \mathrm{m}\)
\(0.450 \; \mathrm{m} - 2(0.333 \; \mathrm{m}) = -0.216 \; \mathrm{m}\)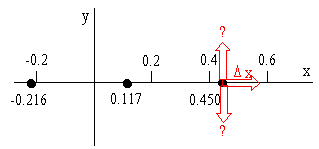
Is \(y\) increasing or decreasing as \(x\) increases by \(\Delta x\) at these points?
Add \(\Delta x\) to \(x\):
\(2.7 \pi - 6 \pi (x + \Delta x)\)decreases because of the negative sign. Therefore, \(\sin[2.7\pi - 6\pi (x + \Delta x)]\) decreases and therefore \(y\) decreases.
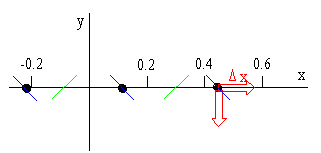
Half way between these points the curve is going the other way.
Final graph:
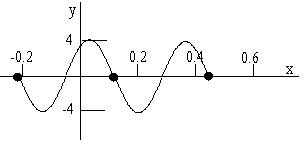
(d) Sketch the graph of the displacement vs. time at a position \(\mathrm {x = 0.400 \;m.}\)
(d)
\(\mathrm {At \;x = 0.400}\)
\(\mathrm {y = 4 \sin[3\pi t - 6\pi (0.4)] = 4 \sin(3\pi t - 2.4\pi)}\)
\(\mathrm {Find\;the \;places \;where\; y = 0}\)\(\mathrm {y = 0 \;when\; \sin (3\pi t - 2.4\pi ) = 0}\)
\(\mathrm {i.e., \;when\; 3p\pi t - 2.4\pi = 0}\)
\(\mathrm {t = 2.4/3 = 0.8\; s}\)
\(\mathrm{Of \;course\; it\; is\; also\; 0 \;every \;T (T = 0.667 \;s, \;see \;part \;b \;above)\; from\; there.}\)
\(\mathrm {i.e., 0.8 - 0.667 = 0.133 \;s}\)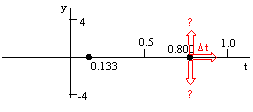
Is \(\mathrm {y}\) increasing or decreasing as \(\mathrm{t}\) is increased by \(\mathrm {\Delta \; t}\) at these points?
\(\mathrm{Add\; \Delta \; t\; to\; t}\)
\(\mathrm {(3p\pi \;t+\Delta \; t -2.4\pi) \;increases.}\)
\(\mathrm {Therefore \;the\; \sin \;increases \;and \;y\; increases.}\)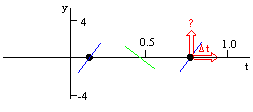
Half way between these points the curve is going the other way.
The complete graph is: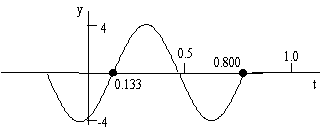
-
The incident wave in problem 10 and the reflected wave \(\mathrm {y = -4 \sin (3\pi\; t + 6\pi \; x)}\) produce a standing wave.
(a) Write the equation of the standing wave.
\(\mathrm {y = -2A\; \cos\omega \; t \ \sin\;kx}\)
\(\mathrm {where: \omega = 3\pi, \;k = 6\pi \;and\; A = 4}\)Therefore
\(\mathrm {y = -8\cos3\pi t\; \sin\; 6\pi \;x}\)(b) Sketch the standing wave at:
(i) t = 0 s
\(\mathrm {y = -8 \cos3\pi \;t \; \sin\;6\pi \; x}\)
\(\mathrm {at \;t = 0, \cos 0 = 1}\)
\(\mathrm {Therefore, \;y = -8 \sin\;6\pi \; x}\)
This is just a negative sine curve with a maximum of 8 and a wave length of 1/3 \(\mathrm {(Remember\; k = 6\pi = 2\pi /\lambda)}\)
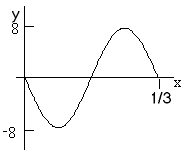
(ii) t = T/4 s
\(\mathrm {y = -8 \cos3\pi \; t \sin\;6\pi \; x}\)
[Remember from above that \(\mathrm {T = 2/3 \;s}\)]
\(\mathrm {at \;t = T/4 = (1/4)(2/3) = 1/6 \;s}\)
\(\mathrm {y = -8 \cos\; 3\pi /6 \sin6\pi \; x}\)
\(\mathrm {= y = -8 \cos\pi /2 \sin6\pi \;x}\)
\(\mathrm {But\;cos\; \pi/2 = 0}\)
\(\mathrm {Therefore \; y = 0 \; everywhere}\)
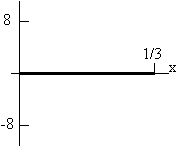
(iii) t = 3/15 s
\(\mathrm {y = -8 \cos\;3\pi \;t \sin6\pi \; x}\)
[Remember from above that \(\mathrm {T = 2/3 s}\)]
\(\mathrm {at\;t = (3/15)T = (3/15)(2/3) = 2/15 \;s}\)
\(\mathrm {y = -8 \cos3\pi (2/15) sin6\pi \; x}\)
\(\mathrm {= -8 \cos0.4\pi \sin6\pi \;x}\)
\(\mathrm {= -8 \cos 72^\circ \sin 6\pi \; x}\)
\(\mathrm {= -2.47 \sin 6\pi \; x}\)
This is just a negative sine curve with a maximum of 2.47 and a wave length of 1/3
\(\mathrm {(Remember\; k = 6\pi = 2\pi /\lambda)}\)
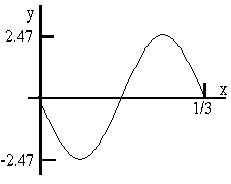
-
An incident wave \(\mathrm {y = -4\sin(3\pi \; t - 6\pi \; x)}\) and a reflected wave \(\mathrm {y = 4 \sin(3\pi\; t + 6\pi \; x)}\) produce a standing wave. What is the equation?
Remember the standard form:
\(\mathrm {y_1 = A \sin(\omega t - kx)}\)
\(\mathrm {y_2 = -A \sin(\omega t + kx)}\)
Produces:
\(\mathrm {y = y_1 + y_2 = -2A\cos \omega t \;\cos\; kx}\)In this case the amplitudes are reversed in sign but not the direction of the waves so only the sign of the standing wave amplitude is reversed.
\(\mathrm {y = 8 \cos \omega t \sin \;kx}\) -
A standing wave of equation \(\mathrm {y = -6\cos 6t \sin \;4x}\) is formed from a reflected wave moving in the \(\mathrm {+x}\) direction, and an incident wave moving in the \(\mathrm {-x}\) direction. What are the equations of the incident and reflected waves?
\(\mathrm {y = -6 \cos 6t \sin \;4x}\)
\(\mathrm {w = 6, k = 4}\)
Reversing the direction of the waves but not the sign of the amplitudes (i.e., incident + and reflected -) would reverse the sign of the standing wave amplitude so it would be \(\mathrm {2 \times 3 = 6.}\)
Since the standing wave amplitude is negative, then the signs of the travelling wave amplitudes must also be reversed.
\(\mathrm {y_i = -3 \sin (6t + 4x) (+ sign \;means \;to \;the\; -x \;direction)}\)
\(\mathrm {y_r = 3 \sin (6t - 4x) (- sign \;means \;to \;the\; +x \;direction)}\)