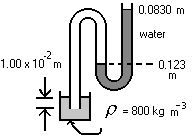Study Guide 13 - Pressure, Denisty and Surface Tension
- What is a pressure of 0.540 Atm in:
(a) \(\mathrm {mm \;Hg}\)
What is the relation between pressure and height of a collumn of incompressible liquid?
\(\mathrm {P = \rho gh}\)
With \(\rho\) in \(\mathrm{kg/m^3,}\) \(\mathrm{h}\) in \(\mathrm {m}\) and \(\mathrm {g = 9.8 \;m/s^2,}\) what are the units of \(\mathrm {P?}\)
Move to part b.
For mercury \(\mathrm {(density = 13600\; kg/m^3) using\; P = \rho gh}\)
\(\mathrm{0.5454 \times 10^5 = 13600(9.8)h \\ h = 0.41\; m = 410\; mm}\)
(b) \(\mathrm {Pa}\)
The unit of pressure in S.I. is "pascal" (Pa), which is \(\mathrm {N/m^2}\)
Now knowing that
\(\mathrm {1 \;Atm = 1.01\times 10^5 \;Pa}\)
we have:
\(\mathrm {0.540\; Atm = 0.540\times 1.01\times 10^5 = 0.5454\times 10^5 \;Pa}\)The answers for parts (a), (c) and (d) can now be determined.
(c) \(\mathrm {m\; H_2O}\)
For water \(\mathrm {(density\; 1000\; kg/m^3)}\)
\(\mathrm {0.5454 \times 10^5 = 1000(9.8)H \\ h = 5.6\; m}\)
(d) \(\mathrm {cm\; blood}\)
For blood \(\mathrm {(density\; 1050 \;kg/m^3)}\)
\(\mathrm {0.5454 \times 10^5 = 1050(9.8)h \\ h = 5.3 m = 530 \;cm}\)
- What is a pressure of \(\mathrm {1.00\; kPa}\) in:
(a) \(\mathrm {m\; Hg}\)
The relationship between pressure and height of a column of incompressible liquid of density \(\rho \) is:
\(\mathrm {P = \rho gh}\)
where \(\mathrm {P}\) is measured in pascals \(\mathrm {(Pa) \;or \;N/m^2.}\)
For mercury, \(\mathrm{\rho = 13600\;kg/m^3}\)
\(\mathrm {1.00\times 10^3 = 13600(9.8)h \\ h = 7.5\times 10^{-3} m = 7.5\; mm}\)
(b) \(\mathrm {Atm}\)
One atmosphere is \(\mathrm{1.01\times 10^5 \;Pa}\)
Therefore \(\mathrm {1.00\times 10^3 \;Pa = 1.00\times 10^3/1.01\times 10^5 = 9.9\times 10^{-3} \;Atm.}\)
(c) \(\mathrm {m \;H_2O}\)
For water, \(\mathrm {\rho = 1000\; kg/m}\)
\(\mathrm {1.00\times 10^3 = 1000(9.8)h \\ h = 0.102\; m}\)
(d) \(\mathrm {cm\; blood ?}\)
For blood, \(\mathrm {\rho = 1050\; kg/m^3}\)
\(\mathrm{1.00\times 10^3 = 1050(9.8)h \\ h = 0.097 \;m = 9.7 \;cm}\)
- The diagram is a schematic representation of that used in some laboratories for water surface tension measurements. What is the gauge pressure indicated by the manometer?
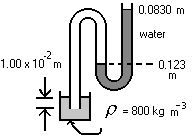
What is the relation between pressure and height of a column of incompressible liquid?
\(\mathrm {P = \rho gh}\)
\(\mathrm {P = (1000)(9.8)(0.123 - 0.083) = 392\; Pa}\)
- Manometers \(\mathrm {M_1}\) and \(\mathrm{M_3}\) are filled with water and \(\mathrm {M_2}\) with kerosene \(\mathrm {(s.g. = 0.820).}\) If \(\mathrm {PA\; is \;1.13 × 10^5 \; Pa\; (gauge):}\)
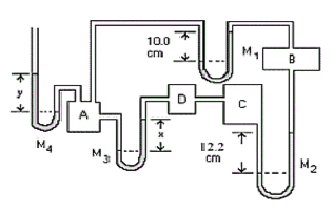
(a) What is \(\mathrm{P_B ; \;P_C ; \;P_D}\) (both gauge and absolute)?
Is the pressure in B; higher than, lower than or the same as that in A?
It is Lower than as can be seen from the manometer \(\mathrm {M_1.}\)
What is the pressure difference P?
\(\mathrm {Pressure \;difference = P = \rho gh \\ P_B = P_A - \rho gh = 1.13 \times 10^5 - (1000)(9.8)(0.10) = 1.12\times 10^5 \;Pa \;(gauge)}\)The absolute pressure is higher than that in chamber B.
\(\mathrm {P_{ABS} = P_{GA} + 1.01 \times 10^5 \;Pa \\ For\; chamber\; B: P_{ABS} = 1.01 \times 10^5 + 1.12 \times 10^5 = 2.13 \times 10^5 \;Pa}\)
The pressure in C higher than that in chamber B.
\(\mathrm {So\; the\; pressure\; in\; C\; is\; P_B + \rho gh \\ P_C = 1.12\times 10^5 + (820)(9.8)(0.122) = 1.13 \times 10^5\; Pa\; (gauge) \\ P_{C, ABS} = 1.01 \times 10^5 + 1.13 \times10^5 = 2.14 \times 10^5 \;Pa.}\)The pressure in D the same as that in chamber C.
Notice that the pressure calculated for C and D is the same as that given for A. This means that x = 0. This is the answer to part (b).
(b) What is the level difference, \(\mathrm{x,}\) in \(\mathrm {M_3 ?}\)
As indicated above \(\mathrm {x = 0.}\)
(c) If \(\mathrm {M_4}\) is filled with mercury, what is the level difference, \(\mathrm {y?}\)
The pressure in A is higher than the atmospheric pressure.
The pressure in A is higher by the amount \(\mathrm {P = \rho gh}\)
Since the gauge pressure in A is \(\mathrm {1.13 \times 10^5 \;Pa,}\) then:
\(\mathrm {\rho gh = 1.13\times 10^5}\)\(\mathrm { H = 1.13 \times 10^5/(13600 \times 9.8) = 0.848\; m = 848 \;mm}\)
- Calculate the height in the atmosphere at which the atmospheric pressure is 0.15 that at sea level. Assume that the molar mass of the air molecules is 29 g/mol, and that the air is at a uniform temperature of 300 K.
The Barometric equation is:
\(\mathrm{ P = P_0e^{-\frac{mgh}{k_bT}}}\)where \(\mathrm {k_B = 1.38\times 10^{-23}}\) J/K is Boltzmann's constant and m is the mass of the average air molecule in kg.
\(\mathrm {m = 29 \times 10^{-3}(kg/mole)/6.02\times 10^{23} (molecules/mole) = 4.82\times 10^{-26} kg}\)Substituting
\(\mathrm {0.15 = e ^{-\frac{(4.82 \times 10^{-26})(98)h}{(1.38 \times 10^{23})(300)}}= e^{- 1.141 \times 10^{-4 h}}}\)
\(\mathrm {\ell n (0.15) = -1.897 = -1.141 x 10^{-4} h}\)
\(\mathrm {h = 16.6 \times 10^3 m = 16.6\; km}\)
- A soap bubble is in a chamber pressurized to 1.20 atmospheres of air (absolute pressure). The bubble is \(\mathrm {1.00 \times 10^{-2} \; mm}\) in diameter. What is the absolute pressure inside the bubble? \(\mathrm {(use\; \gamma = 7.30 \times 10^{-2} \;N/m)}\)
How many surfaces does this soap bubble have?
It has 2, an inside and an outside air-water interface.
What is the excess pressure inside such a bubble?
\(\mathrm{4\gamma /r}\)
There is \(\mathrm {2\gamma/r}\) for each surface so;
\(\mathrm {\Delta P = 4\gamma /r = 4(7.30\times 10^{2)}/0.50\times 10^{-5} = 0.584\times 10^5 \;Pa}\)The total pressure inside the bubble \(\mathrm {= P_{out} + \Delta P}\)
\(\mathrm {= 1.2 \times 1.01\times 10^5 + 0.584\times 10^5 = 1.80\times 10^5 \;Pa \\ = 1.80\times 10^5/1.01 \times 10^5 = 1.78\; Atm}\)
- The soap solution (s.g. = 1.00) used to make the bubble in question #6 is standing in an open vertical tank.
(a) How far below the surface must a bubble be to experience the same external pressure as in question 6?
To achieve a pressure of 1.2 Atm. in an open tank the liquid column must provide 0.2 Atm since the atmosphere already provides 1 Atm.
\(\mathrm {\rho gh = (1000)(9.8)h = 0.2 \times 1.01 \times 10^5 \\ h = 2.06\;m}\)
(b) If the bubble is \(\mathrm {1.00 \times 10^2\; mm}\) in diameter, what is the absolute pressure inside the bubble?
How many surfaces does this soap bubble have?
It has only one air-water interface.
Therefore \(\mathrm {\Delta P = 2\gamma /r = 2(7.30 \times 10^{-2})/0.5 \times 10^{-5} = 0.292 \times 10^5 \;Pa}\)The external pressure on the bubble is \(\mathrm {1.2\;Atm. = 1.2 \times 1.01\times 10^5 = 1.212 \times 10^5 \;Pa}\)
The total absolute pressure inside the bubble =
\(\mathrm {1.212 \times 10^5 + 0.292 \times 10^5 = 1.50 \times 10^5 \;Pa}\)
- Two soap bubbles are floating around in air. One is twice the volume of the other. The excess pressure inside the larger bubble is approximately That inside the smaller bubble.
\(\mathrm {\Delta P_L/\Delta P_S = (4\gamma /r_L)/(4\gamma /r_S) = r_S/r_L}\)
\(\mathrm {V_S/V_L = (r_S/r_L)^3 = 1/2}\)
\(\mathrm {r_S/r_L = (1/2)^{1/3} = 0.79}\)
Therefore \(\mathrm {\Delta P_L/\Delta P_S = 0.79}\)

(a) The figure shows a drop of liquid on glass. Is the contact angle greater than 90 or less than 90?
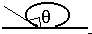
The angle is indicated in the figure; it is greater than \(\mathrm {90^\circ}\).
(b) If a glass tube were dipped in a beaker of the liquid, would the liquid rise up the tube (capillary rise) or go down in the tube (capillary fall)? Give your reasoning. (Be brief.)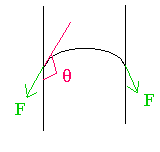
The angle greater than 90 degrees is shown in red
The direction of the surface tension force is shown in green. It will pull the surface down.