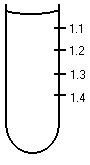Study Guide 16 - Boltzmann's Equation and Sedimentation
- A gas in a container is at a constant temperature \(\mathrm {T.}\) The molecules have two vibrational energy states, the higher of which has energy \(\mathrm {0.88\; k_BT.}\) There are 3000 molecules in this higher energy state and approximately 5500 in the lower state. What is the energy of the molecules in the lower state?
Let \(\mathrm {N_0}\) be the number of molecules in the ground state with average energy \(\mathrm {k_BT.}\)
Let \(\mathrm {N_H}\) be the number of molecules in the higher state with average energy \(\mathrm {0.88\;k_BT.}\)
Let \(\mathrm {N_L}\) be the number of molecules in the ground state with average energy \(\mathrm {ck_BT.}\)\(\mathrm {N_H = N_0e^{-0.98} = 3000\\ N_L = N_0e ^{- \tau} = 5500 \\ \frac{3000}{5500} = \frac{e^{-0.88}}{e^{-\tau}}\\ e^{-\tau} = \frac{55}{30}e^{-0.88} = 0.76 \\ Take\; logarithms \\ c = 0.27 }\)
Therefore the energy in the lower state is \(\mathrm {0.27\;k_BT}\)
- Spherical particles have a density of \(\mathrm {1.30 \times 10^3\; kg\; m^3}\) and radius of \(\mathrm {0.22 \times 10^6\; m.}\)
(a) What is their mass?
\(\mathrm{Mass = volume \times density = (4/3)\pi r^3 \times r}\)
\(\mathrm {Mass = (4/3)\pi (0.22\times 10^{-6})3 \times 1.30 \times 10^3 = 5.8 \times10^{-17}\; kg}\)
(b) What is their apparent weight in water?
Apparent weight = Weight - Weight of displaced fluid (this is Archimedes Principle)
\(\mathrm {Mass\; of\; displaced\; water = (4/3)\pi r^3 \times \rho _{water} = (4/3)\pi(0.22 \times 10^{-6})3 \times 1\times 10^3 = 4.46 \times 10^{-17} \;kg}\)From part (a) we saw that the mass of the particle was \(\mathrm {5.8 \times 10^{-17} \;kg}\)
\(\mathrm {Therefore\; the\; apparent\; weight = (5.8 \times 10^{-17}\;kg - 4.46 \times 10^{-17}\;kg) \times g = 1.3 \times10^{-16}\; N}\)
- An ice cube of density \(\mathrm {917\; kg\; m^3}\) floats in a martini of density \(\mathrm{925\; kg\; m^3.}\) What fraction of the ice cube is submerged?
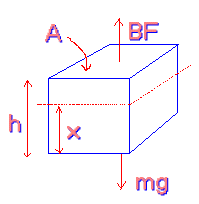
In equilibrium
\(\mathrm {BF = mg }\)\(\mathrm {Therefore: \rho _fg(Volume\; submerged) = \rho g(Volume) \\ \rho _fAx = \rho(Ah) \\ x/h = \rho/\rho_f = 917/925 = 0.99}\)
- In an experiment similar to Perrin's, 120 particles per unit volume are counted at the bottom of a container. 80 particles per unit volume are counted at a height of 5.00 cm above this. At what height above the bottom of the container will there be 40 particles per unit volume?
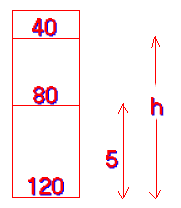
The particles in a Perrin-type experiment obey the Barometric equation
\(\mathrm {\frac{N}{N_0} = e^{-mgh/kT}}\)where the only variable is \(\mathrm{h.}\) Thus we can write:
\(\mathrm {N/N_0 = e^{-qh},}\) where \(\mathrm {q}\) is a constant.
Between the bottom and h = 5 cm:
\(\mathrm {N_5/N_0 = 80/120 = e^{-q(5)}\\ ln\; 80/120 = -q(5)\\ q = 0.081\; cm^{-1}}\)
Between the bottom and height h:
\(\mathrm {N/N_0 = 40/120 = e^{-0.081h} \\ ln \;40/120 = -0.081h \\ h = 13.6 \;cm}\)
- Which of the following represents a sketch of terminal velocity vs. diameter of the sedimenting particle?
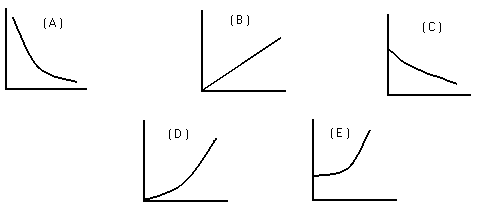
Equation (11-25) of the text gives for the terminal velocity:
\(\mathrm{v_t = \frac{2}{9}\frac{r^2g}{\eta}('o_5 - ,o_{\ell})}\)so \(\mathrm {v_t \sim r^2 \sim d^2}\)
i.e., \(\mathrm {v_t}\) increases faster than linearly with \(\mathrm {d,}\) so either answer \(\mathrm {D}\) or \(\mathrm {E}\) is indicated. Further if \(\mathrm {d = 0 (r = 0)}\) then \(\mathrm {v_t = 0}\) so the answer is \(\mathrm {D.}\)
- When a sedimenting particle reaches its terminal velocity, which of the following is true?
(\(\mathrm{F_g = weight \;of \;particle;}\) \(\mathrm {F_b = buoyant\; force;}\) \(\mathrm {F_v = frictional\; force}\))
(a) \(\mathrm {F_g + F_b = F_v}\)
(b) \(\mathrm {F_g + F_v = F_b}\)
(c) \(\mathrm {F_g > F_v + F_b}\)
(d) \(\mathrm {F_g = F_v +F_b}\)
(e) \(\mathrm{F_g + F_b < F_v}\)
When the particle is at terminal velocity its acceleration is zero, so the net force is zero.
\(\mathrm {F_g}\) is moving the particle down due to gravity. \(\mathrm {F_b}\) is the buoyant force and acts up as does \(\mathrm {F_v}\) since viscosity always acts to oppose the motion.
Therefore \(\mathrm {F_g = F_v + F_b,}\) i.e., answer (d)
- A protein of molar mass \(\mathrm {6.0 \times 10^6 \;g \;mol^{-1}}\) and density \(\mathrm {1.33 \times 10^3 kg\; m^{-3}}\) is in an ultracentrifuge tube (filled with water) at a distance of \(\mathrm {10\; cm}\) from the rotation axis. The rotor is spinning at \(\mathrm {60000\; rpm.}\) What is the centrifugal "force" on a protein molecule?
Equation 9-4of the text gives for the centripetal acceleration
\(\mathrm {a_c = v^2/r}\)
\(\mathrm {The\; centripetal\; force = F_c = ma_c = mv^2/r = (M/N_A)v^2/r}\)
where \(\mathrm {M}\) is the molar mass and \(\mathrm {N_A}\) is Avogadro's number.
From equation 9-6 in the text
\(\mathrm {v = 2\pi rf \\ F_c = (M/N_A)(2\pi rf)^2/r = (M/N_A)4\pi^2rf^2 \\ f = 60000/60 = 1000\; Hz}\)
\(\mathrm {F_c = (6.0\times 10^6 \times 10^{-3}/6.02 \times 10^{23})4\pi^2(0.1)(1000)2 = 3.9 \times 10^{-14} N}\)
- A centrifuge tube is filled with a cesium chloride solution prepared in such a way that there is density gradient down the tube, i.e., the solution is more dense towards the bottom of the tube. The figures on the diagram indicate the specific gravity at various points.
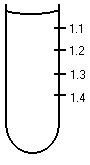
Some polysaccharide of density \(\mathrm {1280\; kg\; m^{-3}}\) is added at the top and the tube is spun at very high speed for a day.
(a) Using the equation
\(\mathrm{v_t = \frac{2}{9} \frac{r^2 g}{\eta} ( \rho_s - \rho_{\ell} )\frac{r^2 "g"}{\eta}}\)
sketch a graph of the terminal speed of the polysaccharide vs. depth in the tube. (Notice that rlchanges linearly with depth.) Assume "g" is constant, independent of depth.The formula for terminal velocity is:
\(\mathrm{v_t = \frac{2}{9}\frac{r^2g}{\eta}(\rho_s - \rho_ \ell)}\)That is \(\mathrm {v_t \sim \rho _s -\rho _l}\)
The graph of \(\mathrm {v_t}\) vs. depth is a straight line of negative slope, since \(\mathrm{\rho _l}\) varies linearly with depth. At \(\mathrm {\rho_s = \rho_l}\) the terminal velocity becomes zero, i.e., \(\mathrm {\rho_l = 1280\; kg/m^3}\)
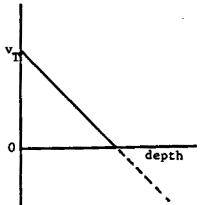
(b) What value of \(\mathrm {\rho_l}\) reduces \(\mathrm {v_T}\) to zero?
The formula for terminal velocity is:
\(\mathrm{v_t = \frac{2}{9}\frac{r^2g}{\eta}(\rho_s - \rho _\ell)}\)That is \(\mathrm {v_t \sim \rho _s -\rho _l}\)
The graph of \(\mathrm {v_t}\) vs. depth is a straight line of negative slope, since \(\mathrm{\rho _l}\) varies linearly with depth. At \(\mathrm {\rho_s = \rho_l}\) the terminal velocity becomes zero, i.e., \(\mathrm {\rho_l = 1280\; kg/m^3}\)

(c) Show on the diagram where the polysaccharide will be found after the day's spinning. Why will it be found there?As determined in part a and b, \(\mathrm{v_t = 0}\) when \(\mathrm {\rho_l = 1280\; kg/m^3.}\)
The particles come to rest at that place.
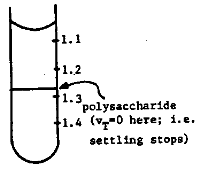
(d) The amount of settling of the cesium chloride in the solution is negligible. Why?Cesium and chloride ions are very small, therefore \(\mathrm {v_t}\) is very small. The thermal motion from the other molecules in the solution maintain the density gradient as in Perrin's experiment.