Study Guide 14 - Fluid Dynamics

  1. An artery of radius \(\mathrm {R_1}\) carries blood with an average linear speed \(\mathrm {v_1.}\) It divides into 3 smaller arteries, each of radius
    \(\mathrm {R_2 = ½R_1.}\) What will be the speed \(\mathrm {v_2}\) of the blood in the smaller arteries, relative to \(\mathrm {v_1?}\)
     

    The equation of continuity says that for an incompressible fluid the volume per unit time must be constant, i.e.,
    \(\mathrm {V_1/t = V_2/t}\)

    If we represent the volume as an area times a distance:
    \(\mathrm {A_1 \times 1/t = A_2 \times 2/t}\)

    But x/t is a velocity, so
    \(\mathrm {A_1v_1 = A_2v_2}\)

    In this problem \(\mathrm {A_2 = 3A´_2,}\) where \(\mathrm {A´_2}\) is the cross-section area of one of the 3 sub-arteries.
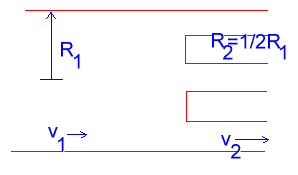
    Diagram indicating cross section of sub-arteries.

    \(\mathrm {A_1v_1 = 3A´_2v_2}\)

    For circular cross-sections, \(\mathrm {A \sim R^2}\)
    \(\mathrm{R_1{^2}v_1 = 3R_2{^2}v_2}\)

    But \(\mathrm {R_2 = ½R_1}\)
    \(\mathrm {R_1{^2}v_1 = 3(¼R_1{^2})v_2 \\ v_2 = (4/3)v_1}\)


     
  2. The capillary tube delivers water by viscous flow from a reservoir and is 0.50 mm in diameter. The time taken to collect \(\mathrm {50\; cm^3}\) of water was 7.0 minutes. How much longer would it take to collect \(\mathrm {50\; cm^3}\) of water if the only change is to decrease the tube diameter to 0.30 mm?
     

    Since this is a problem of viscous flow which law is involved?

    This problem involves Poiseuille"s equation, i.e.,

    \(\mathrm{Q = \frac{\pi r^4 \Delta P}{8 \eta \ell}\\ \frac{V}{t_1} = \frac{\pi r_1{^4} \Delta P}{8 \eta \ell} \\ \frac{V}{t_2} = \frac{\pi r_2{^4} \Delta P}{8 \eta \ell} \\ \frac{t_2}{t_1} = \bigg ( \frac{r_1}{r_2} \bigg)^4 \\ t_2 = \bigg( \frac{r_1}{r_2}\bigg)^4 t_1 = \bigg (\frac{5}{3} \bigg) ^4 \times 7 = 54 \; min} \)

    The increase in time = 54 - 7 = 47 min.


     
  3. The aorta in the diagram has a constriction which reduces its cross-sectional area from A to A/3. Assuming the blood has zero viscosity, calculate the pressure difference \(\mathrm {(P_L - P_S)\; in \;Nm^{-2},}\) between the large and small regions of the aorta.

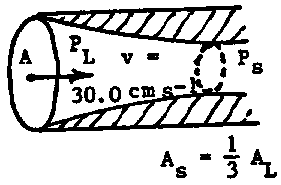
    Diagram of aorta

    This is a problem of non-viscous flow. Which law is involved?

    Bernoulli's equation which states:
    \(\mathrm {P + ½\rho v^2 +\rho gh = constant}\)
    or relating the conditions at two places:
    \(\mathrm {P_1 + ½\rho v_1{^2} + \rho gh_1 = P_2 + ½\rho v_2{^2} +\rho gh_2}\)
    For a level pipe \(\mathrm {h_1 = h_2}\)
    \(\mathrm {P_1 + ½\rho v_1{^2} = P_2 + ½\rho v_2{^2}}\)

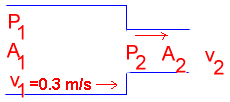
    diagram indicating flow

    In this case \(\mathrm {A_2 = (1/3)A_1}\) and so the equation of continuity gives:
    \(\mathrm {A_1v_1 = A_2v_2 = (1/3)A_1v_2 \\ v_2 = 3v_1}\)

    \(\mathrm {P_1 + ½\rho v_1{^2} = P_2 + ½\rho (9v_1)^2 \\ P_1 - P_2 = ½\rho(9v_1{^2} - v_1{^2}) = ½\rho 8v_1{^2} = 4\rho v_1{^2} \\ = 4(1000)(0.3)^2 = 360\; Pa}\)