Study Guide 6 - The Observed Absorption and Emission of Light by Molecules
- Seventy five percent of the light striking a chlorophyll sample is absorbed. What is the percent transmittance and the absorbance of the sample?
If 75% is absorbed then 25% is transmitted.
\(\mathrm {I/I_0 = 0.25}\)
\(\mathrm {A = \log I_0/I = \log (1/0.25) = \log 4 = 0.60}\) - Convert an absorbance of 0.37 to % transmittance.
\(\mathrm {A = 0.37 = \log I_0/I \\ I_0/I = 2.34 \\ I/I_0 = 1/2.34 =0.427 \\ \%T = 43\%}\)
- A solution yields a %T of 48 in a sample cell with a 1.0 cm path length. What would the %T value be if the same solution were placed in a sample cell with a path length of 3.0 cm?
The only thing that relates directly to sample length and concentration is the absorbance \(\mathrm {A = \varepsilon c\ell,}\) so A must be found.
\(\mathrm {\%T = 48, therefore\; I/I_0 = 0.48 \\ A = \log(1/0.48) = 0.319 = \varepsilon c\ell}\)
\(\mathrm {If\; \ell \;is \;increased\; by\; a\; factor\; 3\; then\; so\; must\; be\; the\; absorbance.}\)
\(\mathrm {A_{new} = 3 \times 0.319 = 0.956 = \log I_0/I \\ I_0/I = 9.04 \\ I/I_0 = 0.11 \\ \%T = 11\%}\) - Sketch:
(Hint: Obtain expressions relating %T and pathlength in both exponential and logarithmic form.)
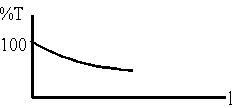
(a) a graph of percent transmittance versus path length.
\(\mathrm {A = \varepsilon c \ell = -\log I/I_0 \\ \frac{I}{I_0}= 10^{\varepsilon c \ell} \\ \frac{I}{I_0}= 10^{-\varepsilon c \ell} \\ \% T = 100(I_0 /I) = 100 \times 10 ^{- \varepsilon c \ell}}\)
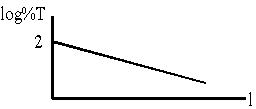
(b) a graph of log %T versus path length.
\(\mathrm {A = \varepsilon c \ell = \log I/I_0 \\ \frac{I_0}{I}= 10 ^{-}}\)
- (a) You have equal volumes of two solutions in two glass cells. Extinction coefficients and concentrations are: \(\mathrm {4200\; litre.mole^{-1}.cm^{-1}}\) and \(\mathrm {3.00\times 10^{-4} \; moles/litre}\) for solution one and \(\mathrm {2800\; litre.mole^{-1}.cm^{-1}}\) and \(\mathrm {2.60\times 10^{-4} \; mole/litre}\) for solution two. The two solutions each having a path length of 1.00 cm are set one behind the other in a light beam. Find the total absorbance of the two solutions.
When such absorbers are combined in any way, what is it that adds?
The absorbances add.
\(\mathrm{A_1 = \varepsilon _1c_1\ell _1 = 4200 \times 3.00\times 10^{-4} \times 1 = 1.26 \\ A_2 = e_2c_2\ell _2 = 2800 \times 2.60 \times 10^{-4} \times 1 = 0.73 \\ A = 1.26 + 0.73 = 1.99}\)
(b) Equal volumes of the two solutions are mixed and some of the mixture is added to a new cell having a path length of 1.00 cm. Calculate the expected percent transmittance of the mixture. (Remember that, when you mix equal volumes, concentrations are halved.
There are 2 ways to reason this question.
(a) As suggested by the hint the concentrations are halved:
\(\mathrm {A_1 = \varepsilon_1c_1\ell_1 = 4200 \times 1.50 \times 10^{-4} \times 1 = 0.630 \\ A_2 = e_2c_2\ell_2 = 4200 \times 1.30 \times 10^{-4} \times 1 = 0.365 \\ A = 0.630 + 0.365 = 0.995}\)
(b) Alternatively you could think of the 1 cm cell as being 1/2 cm of the 1st solution and 1/2 cm of the 2nd solution.
Therefore \(\mathrm {A = 1.00/2 = 0.995}\) as before.In either case:
\(\mathrm {A = 0.995 = \log I_0/I \\ I_0/I = 9.89 \\ \%T = 100 \ell /I_0 = 100/9.89 = 10.1\%}\) - Typical visible, infrared and microwave wavelengths are, respectively, \(\mathrm {500 \;nm, 5.0\; \mu m, 5.0\; mm.}\) Calculate the ratio \(\mathrm {E_r/E_e, E_v/E_e, and E_r/E_v.}\) (r = rotation, v = vibration, e = electronic)
Rotation energies are the lowest and therefore, from \(\mathrm {\lambda = hc/E (E = hc/ \lambda)}\) involve the longest wavelength, i.e., 5.0 mm.
Electronic energies are the highest and therefore involve the shortest wavelength, i.e., 500 nm.The vibrational energies are in between as are the wavelengths, i.e., 5.0 mm.
Since \(\mathrm {E_1/E_2 = \lambda_2/ \lambda_1}\) (from the above equation).
\(\mathrm {Then\; E_r/E_e = 500\times 10^{-9}/5.0\times 10^{-3} = 10^{-4} \\ E_v/E_e = 500 \times 10^{-9}/5.0 \times 10^{-6} = 10^{-1} \\ E_r/E_v = 5.0 \times 10^{-6}/5.0 \times 10^{-3} = 10^{-3}}\)
- A molecule absorbs a photon of wavelength \(\mathrm {\lambda_a.}\) The molecule both fluoresces with wavelength lf and phosphoresces with wavelength \(\mathrm {\lambda_p.}\) Arrange these three wavelengths in order of increasing wavelength.
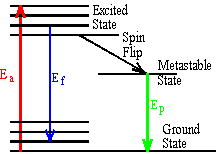
The figure shows a ground state and an excited electronic state with a few vibrational levels.
It is clear that \(\mathrm {E_f < E_a}\)
Therefore \(\mathrm {\lambda_f >\lambda_a}\)
The metastable state is always significantly lower in energy than the excited state so \(\mathrm {E_p < E_f}\)
Therefore \(\mathrm {\lambda_p >\lambda_f}\)In order of increasing wavelength: \(\mathrm {\lambda_a, \lambda_f, \lambda_p}\)
- A sample is irradiated with a burst of light in a parallel beam of which contains \(\mathrm {1.0 x 10^{18}}\) photons. The wavelength of the photons is 500 nm and the absorbance of the example is 0.680.
(a) How many photons are in the transmitted flash and what is their wavelength?
If the initial beam has \(1\times 10^{18}\) photons \(\mathrm {( I_o= 1 \times 10^{18})}\) and the absorbance is 0.680, then
\(\mathrm {A = \log (I_o/I)}\)\(\mathrm {antilog \; 0.680 = 1 \times 10^{18} \;photons / I}\)
\(\mathrm {I = 2.09 \times 10^{17} \; photons}\)
Therefore the number of photons transmitted is \(\mathrm {2.09 \times 10^{17}.}\)
What is the wavelength of the transmitted photons?
1) longer than the initial beam.
2) the same as the initial beam - The transmitted beam has no interaction with the sample, to the wavelength is still 500 nm.
3) shorter than the initial beam.
(b) If the number of photons is conserved (quantum efficiency = 1), then how many photons are fluoresced?
Since the number of photons is conserved (one photon emitted for every one that is absorbed) the number of photons in the initial beam equals the number transmitted plus the number fluoresced.
In part a) the number of photons transmitted was found to be \(2.09 \times 10^{17}.\)So, the number of photons fluoresced is:
\(\mathrm{1.0 \times 10^{18} \; photons - 2.09 \times 10^{17} \; photons\\ = 7.91 \times 10^{17} \; photons}\)
(c) The wavelength of the fluoresced photons is 700 nm. How much heat (J) is deposited in the sample?In this process energy is conserved.
Let the absorption wavelength be \(\mathrm {\lambda_{500}.}\) What is an expression for the energy that enters the sample?
\(\mathrm {10^{18} hc / \lambda _{500}}\)
The situation is shown in the figure.
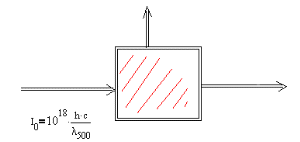
This energy ends up in three ways:
(1) Transmitted photons
(2) Fluoresced photons
(3) Heat left in the sample.
\(\mathrm {E_o}\) is the energy of the initial photons, \(\mathrm {E_t}\) is the energy of the transmitted photons, \(\mathrm {E_f}\) is the energy of the fluoresced photons, and H is the heat left in the sample.What is the correct expression for conserving energy?
\(\mathrm {E_o = E_t + E_f + H}\) OR \(\mathrm {E_o - E_t = E_f - H}\)
\(\mathrm {E_o = E_t + E_f + H}\) is the correct expression.
We know the number of photons in each energy term (the total is given, and the # transmitted and fluoresced have been solved for in a) and b)) and we also know all of the of the wavelengths of these photons, so we now can solve for the heat left in the sample
\(\mathrm {10^{18} \frac{hc}{500 \times 10^{_9} }= 7.91 \times 10^{17} \frac{hc}{700 \times 10^{-9}}+ 2.1 \times 10^{17} \frac {hc}{500 \times 10^{-9}}+H \\ \frac{7.9 \times 10^{17} hc}{10^{-7}}\Biggl( \frac{1}{5} - \frac{1}{7}\Biggr)= 0.09 \; J}\)Therefore the heat left in the sample is 0.09 J.



