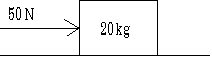Study Guide 10 - Mechanics of Biological Systems: Forces and Motion
- The surface is frictionless. What is the acceleration of the 20 kg mass?
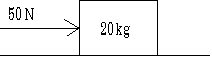
\(\mathrm{F = ma \\ 50 = 20a \\ a = 50/20 = 2.5 \;m/s^2}\)
- The surface is frictionless. What is the acceleration of the 20 kg mass?

Is there any unbalanced force in the vertical direction?
No.
Is the force that accelerates the block: \(\mathrm {F}\) or \(\mathrm {F\; \cos\; 36.9}\) or \(\mathrm {F\; \sin \;36.9 ?}\)
The horizontal component of \(\mathrm {F = 50\; \cos \;36.9 = 50 \times 0.8 = 40\; N}\)
\(\mathrm {F = ma}\)
\(\mathrm {a = F/m = 40/20 = 2.0 m/s}\)
- A 10 kg mass is sliding across a smooth (frictionless) floor at 20 m/s. What force, opposite to the motion, will bring it to a halt in 5 s?
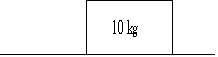
First find the required acceleration.
\(\mathrm {v = v_0 + at \\ a = (0 - 20)/5 = -4.0 m/s^2}\)
\(\mathrm {F = ma = 10 \times (-4.0) = -40\; N}\)
- A person has mass 50.0 kg. What is her weight
(a) on the Earth?
\(\mathrm {On \; Earth, W = mg = 50.0 \times 9.80 = 4.90 \times 10^2 \; N}\)
(b) on the surface of Mars? Mars has a mass of \(\mathrm {6.46 \times 10^{23}\; kg}\) and an average radius of approximately \(\mathrm {3.40 \times 10^6\; m}\).
On Mars the effective \(\mathrm {g}\) is less.
Since gravitational attraction varies with the product of the masses invomved and inversely as the square of the distance (in this case the radii of the planets) then
\(\mathrm {g_{Mars} = g_{Earth}(M_{Mars}/M_{Earth})(R_{Earth}/R_{Mars})^2 \\ = (9.8) \times (6.46\times10^{23}/6.0\times10^{24})(6.37\times 10^6/3.40\times 10^6)2 = 3.7\; m/s^2 \\ W = mg_{Mars} = 50 \times 3.7 = 185\; N}\)
- A car is stuck in the mud. The driver attaches a cable to a tree 50.0 m away and pulls the cable aside at its centre point. If he draws the cable aside 10.0 cm with a 500 N force, what force is exerted on the car? Notice that the angle is very small.
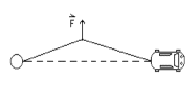
The point where F attaches to the cable is a point which is in equilibrium, i.e., \(\mathrm {\sum F = 0.}\)
How many forces are acting at that point?
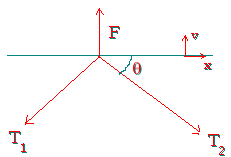
There are 3 forces acting at the point. These are: F and the tension T in the cable acting toward the car and toward the tree.
\(\mathrm {\sum F_x = 0 \\ T_2\; \cos \; \theta - T_1 \; \cos \; \theta = 0 \\ Therefore,\; T_1 = T_2 = T}\)
\(\mathrm {\sum F_y = 0 \\ F - 2T \; \sin \; \theta = 0}\)
Remember that the angle is small so:
\(\mathrm {\sin \; \theta = \theta = 0.1/25 \\ T = F/2 \sin\theta = 500/(2 \times 0.1/25) = 6.25\times 10^4 \;N}\)
- The system is in translational equilibrium. What is the angle and the magnitude of R?
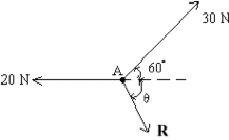
Vertical components (y)
\(\mathrm {30\; \sin \;60 - R\; \sin \theta = 0}\)
\(\mathrm {R\; \sin \theta = 30\; \sin\; 60 = 26 \qquad [1]}\)Horizontal components (x)
\(\mathrm {30\; \cos\; 60 + R\; \cos \theta = 20}\)
\(\mathrm {R\; \cos \theta = 20 - 30\; \cos\; 60 = 5 \qquad [2]}\)Divide [1] by [2]
\(\mathrm{\tan \theta = 26/5 = 5.2}\)
\(\mathrm {\theta = 79.1^\circ}\)From [1]
\(\mathrm {R = (30\; \sin \;60)/(\sin\; 79.1) = 26.5 \;N}\)
- A man drags a 200 kg packing case across a floor with a force of 50.0 N directed at 30.0 to the horizontal. He imparts an acceleration of 0.100 m/s2 to the case. A frictional force opposes him.
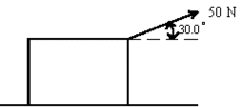
(a) What is its magnitude?
We must first make a free-body diagram of the packing case.
The forces acting on the case are:- The 50 N force at 30º which can be divided into 2 components:
a: 50 cos 30 to the right
b: 50 sin 30 up - The force of friction acting to the left.
- The normal reaction of the floor acting up.
- The weight of the case 200g acting down.
The free-body diagram is therefore:
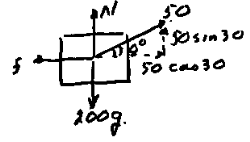
What is the acceleration of the packing case in the vertical direction?
(a) \(\mathrm {0.100\; m/s^2}\) - No. That is the horizontal acceleration.
(b) \(\mathrm {9.8 \;m/s^2}\) - No. That is the acceleration of an object in free-fall.
(c) 0 - Correct! The case does not accelerate in the vertical direction.Therefore in this direction the sum of the forces is zero.
\(\mathrm {\sum F = 0}\)\(\mathrm {N + 50\; \sin \; 30 - 200\; g = 0}\)
\(\mathrm{N = 1960 - 25 = 1935\; N }\) - this is the answer to part b
The acceleration in the horizontal direction is \(\mathrm {0.100 \;m/s^2.}\) The sum of the forces in the horizontal direction is given by:
\(\mathrm {\sum F = ma}\)\(\mathrm {50\; \cos \;30 - f = 200(0.100)\\ f = 43.3 - 20 = 23.3\; N}\)
(b) What is the normal force of the floor on the case?
\(\mathrm{N = 1960 - 25 = 1935\; N }\)
- The 50 N force at 30º which can be divided into 2 components:
- What is the apparent weight of a 60.0 kg person in an elevator
(a) descending at constant velocity?
When an object moves at constant velocity there is no net force (Newton's 1st law).
Therefore the persons apparent weight, which is the force the elevator floor exerts upward on the person
equals the persons own weight acting downward, i.e.,
\(\mathrm {App\; Wt = mg = 60 \times 9.8 = 588 \;N}\)
(b) descending with a downward acceleration of \(\mathrm {1.60\; m/s^2?}\)
If the apparent weight is F (the force the elevator floor exerts upward on the person) then
\(\mathrm {mg - F = ma}\) where \(\mathrm {a}\) is the persons acceleration\(\mathrm {F = m(g - a) = 60 (9.8 - 1.6) = 492 \;N}\)
- A 100 kg crate slides down a plane inclined at 37.0 to the horizontal. If the surface is frictionless,
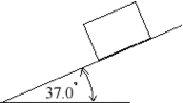
(a) what is the acceleration of the crate?
The component of force down the plane is \(\mathrm {mg \; \sin \; 37}\) and from Newton's second law this must equal \(\mathrm {ma}\)
\(\mathrm {mg\; \sin \; 37 = ma \\ a = g\; \sin \;37 = 9,\;8 \times 0.6 = 5.9 m/s^2}\)
(b) what is the normal force on the crate due to the incline?
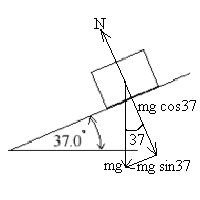
There is no acceleration perpendicular to the plane so
\(\mathrm {N - mg\; \cos \;37 = 0}\)
\(\mathrm {N = 100 \times 9.8 \times 0.8 = 784\; N}\)
- A sled of mass 5.0 kg is being pulled along ice by a force of 10 N which is applied at an angle of 37 up from the horizontal. The kinetic coefficient of friction between sled and ice is 0.10. What is
(a) the acceleration;
\(\mathrm {\sum F_y = 0 \\ N + 10\; \sin \;37 - mg = 0 \\ N = mg - 10\; \sin \;37 = 5(9.8) - 10(0.6) = 43\; N \\ f = \mu N = 0.1 \times 43 = 4.3 \;N}\)
\(\mathrm {\sum F_x = ma \\ 10\; \cos \;37 - f = ma}\)\(\mathrm {a = (1/5)[10(0.8) - 4.3] = 0.74 \;m/s^2}\)
(b) the speed after 5 seconds if it starts from rest?
\(\mathrm {v = v_0 + at = 0 + 0.74 \times 5 = 3.7 \;m/s}\)
- The 20.0 kg crate is being pushed up the inclined plane by the 200 N force as shown. The coefficient of kinetic friction is 0.200. What is the acceleration of the crate?
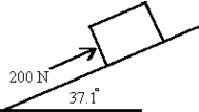
Perpendicular to the plane
\(\mathrm {\sum F = 0 \\ N - mg\; \cos \;37.1 = 0 \\ N = mg\; \cos \; 37.1 \\ f = \mu N = 0.2 \times 20 \times 9.8 \times 0.8 = 31.36 \;N}\)
Along the plane
\(\mathrm {\sum F = ma \\ 200 - mg\; \sin \;37.1 - f = ma \\ 200 - (20)(9.8)(0.6) - 31.36 = 20a \\ a = 51.04/20 = 2.55 \;m/s^2}\)
- A baseball player running with speed 9.00 m/s slides into second base through a distance of 4.00 m. Find the coefficient of kinetic friction. His speed is zero when he touches the base.
\(\mathrm{v^2 = v{_0}^2 + 2ax \\ 0 = 9^2 + 2a4 \\ a = -10.125 m/^2}\)
\(\mathrm {f = ma = \mu mg}\)
\(\mathrm {a = \mu g}\)\(\mathrm {\mu = a/9 = 10.125/9.8 = 1.03}\)
- A car of mass 1000 kg and a truck of mass 2000 kg collide as shown. With what velocity and in what direction will the tangled wreckage move immediately after the collision? Is energy or momentum conserved?
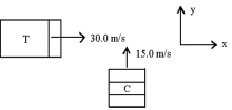
Momentum is conserved in all collisions
Both the magnitude and the direction of the momentum are conserved.
Now conservation of momentum can be applied to the horizontal (x) and vertical (y) components of the momentum independently
Before Collision After Collision \(\mathrm{p_x = 2000 \times 30 \\ p_y = 1000 \times 15}\) 
\(\mathrm {p_x = 3000\; v \cos\; \theta \\ p_y = 3000\; v\; \sin \theta}\)In the x direction: \(\mathrm {3000\; v \sin \theta = 1000 \times 15}\)
In the y direction: \(\mathrm {3000\; v \cos \theta = 2000 \times 30}\)
Divide the first equation by the second:
\(\mathrm {\tan \theta = 15/2\times 30 = 0.25 \\ \theta = 14^\circ}\)\(\mathrm {3000\; v \cos\; 14 = 2000 \times 30 \\ v = 20.6\; m/s}\)
- A box of mass 4.00 kg is pulled a distance of 3.00 m up a 30.0 incline by a force of 100 N applied parallel to the incline. The coefficient of kinetic friction is 0.100. How much work is done by the 100 N force in moving the box the 3.00 m distance?
The problem asks only for the work done by the applied force.
\(\mathrm {W = Fd = 100 \times 3 = 300 \;J}\)
- All surfaces are frictionless. The blocks are initially at rest. The larger block is released and slides down to strike the smaller. They stick together when they collide. What will be their final speed?
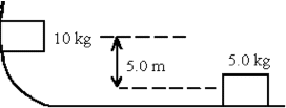
In the frictionless fall of the 10 kg mass what is conserved, Energy or Momentum?
Energy
Potential energy is converted into kinetic energy.
\(\mathrm {mgh = ½mv^2 \\ v = (2gh)^½ = [2(9.8)5]^½ = 9.9 \;m/s}\)
In the subsequent collision with the 5 kg mass what is conserved, Energy or Momentum?
Momentum
Momentum is always conserved in a collision but energy may, or may not be conserved.
\(\mathrm {Momentum\; before\; = mv = 10(9.9) \\ Momentum\; after = MV = (10 + 5)V = 15V \\ 15V = 99 \\ V = 99/15 = 6.6 \;m/s}\) - A motor raises a 100 kg object 40.0 m in 30.0 s. Assume the motor is 100% efficient. What power does it develop?
\(\mathrm {Change\; in \;potential \;energy = mgh = 100(9.8)(40) = 39200 \;J}\)
\(\mathrm {Power = E/t = 3920/30 = 1.31\times 10^2\; J}\)