Study Guide 17 - Random Walk, Diffusion and Osmosis
- A scientist is investigating the one-dimensional diffusion of particles along a thin microtubule (a tube with very small diameter). By analyzing diffusion over a time of 30 seconds, he obtained the following table of displacements:
Number of Particles Approximate displacement in micro meters 10 -50 35 -25 50 0 35 25 10 50
(a) What is the mean displacement of the particles?
\(\mathrm{x(\mu m)}\) \(\mathrm{n}\) \(\mathrm{nx(\mu m)}\) \(\mathrm{nx^2(\mu m^2)}\) -50 10 -500 25000 -25 35 -875 21875 0 50 0 0 25 35 875 21875 50 10 500 25000 \(\mathrm{\overline x= \frac{\sum nx}{\sum n} = \frac{(-500\mu m)+(-875 \mu m)+ 0 \mu m +(875 \mu m)+(500 \mu m)}{10 + 35+50+35+10}= 0\mu m}\)
(b) What is the mean square displacement of the particles?
\(\mathrm{x (\mu m)}\) \(\mathrm{n}\) \(\mathrm{nx(\mu m)}\) \(\mathrm{nx^2(\mu m^2)}\) -50 10 -500 25000 -25 35 -875 21875 0 50 0 0 25 35 875 21875 50 10 500 25000 \(\mathrm{\overline {x^2} = \frac{\sum nx^2}{\sum n}= \frac{25000\mu m^2 + 21875 \mu m^2 + 0 \mu m^2 +21875 \mu m^2+25000 \mu m^2}{10+35+50+35+10}= 670\; \mu m^2 \times \bigg(\frac{1\times 10^{-6}m}{1\mu m}\bigg)^2 = 6.7 \times 10 ^{-10}\;m^2}\)
(c) What is the diffusion coefficient of the particles?
For diffusion in one dimension the relation between \(\mathrm{R_{av}{^2}}\) and \(\mathrm{D}\) is \(\mathrm{R_{av}{^2} = 2Dt}\)
\(\mathrm{D = R_{av}{^2}/2t = 6.7\times 10^{-10}/2 \times 30 = 1.1 \times10^{-11} m^2/s}\)
- A spherical virus has a radius of \(\mathrm{40\; nm.}\) What is the expected diffusion coefficient of such a particle in water at \(\mathrm{20^\circ C?}\)
The molar mass is given by equation 11-19 in the text:
\(\mathrm{M = \rho \frac{4}{3}\pi \bigg(\frac{kT}{6 \pi \eta D }\bigg)^3 N_A}\)
From which:
\(\mathrm{\frac{M_A}{M_B}= \frac{\rho _A}{\rho _B}\bigg(\frac{D_B}{D_A}\bigg)^3 = \frac{115}{0.95}\bigg(\frac{4.7}{7.0}\bigg)^3}\)
- Two spherical enzymes, \(\mathrm{A}\) and \(\mathrm{B,}\) have respective diffusion coefficients of \(\mathrm{7.0\times 10^{-11}m^2/s}\) and \(\mathrm{4.3\times 10^{-11}m^2/s.}\) Their densities are
\(\mathrm{\rho A = 1.15 \times 10^3\; kgm^{-3},}\) \(\mathrm{\rho B = 0.95\times 10^3\; kgm^{-3}.}\) What is the ratio of their molar masses?
The molar mass is given by equation 11-19 in the text:
\(\mathrm{M = \rho \frac{4}{3}\pi \bigg(\frac{kT}{6 \pi \eta D }\bigg)^3 N_A}\)
From which:
\(\mathrm{\frac{M_A}{M_B}= \frac{\rho _A}{\rho _B}\bigg(\frac{D_B}{D_A}\bigg)^3 = \frac{115}{0.95}\bigg(\frac{4.7}{7.0}\bigg)^3 \\ = 0.28}\)
- The diffusion coefficient for sodium ions crossing a biological membrane \(\mathrm{10\; nm}\) thick is \(\mathrm{1.0\times 10^{-18} m^2/s.}\) What flow rate of sodium ions would move across an area \(\mathrm{10\; nm \times 10\; nm}\) if the concentration difference across the membrane is \(\mathrm{0.50\; mol/dm^3?}\)
Fick's law of diffusion states:
\(\mathrm{\frac{dn}{dt}= -DA\frac{dc}{dx}}\)where dn/dt is the quantity of matter per unit time crossing an area A with a diffusion coefficient D, driven by a concentration gradient dc/dx.
\(\mathrm{dc = 0.5\; moles/dm^3(1000dm^3/m^3) = 500\; mol/m^3 \\ |dn/dt| = 1\times10-8[10\times 10^{-9} \times 10X10-9]500/10 \times 10^{-9} \\ = 5 \times10^{-24}\; mol/s}\)
- The diffusion coefficient of potassium across the same membrane is 100 times greater than for sodium. If the concentration on one side is \(\mathrm{150\; millimoles\; per\;dm^3}\) and on the other is \(\mathrm{5\; millimoles\; per\; dm^3,}\) what would be the potassium flow rate across \(\mathrm{5.0\; nm^2}\) of the membrane?
Using Fick's law of diffusion as described in Question 4:
\(\mathrm{\frac{dn}{dt}= = -DA \frac{dc}{dx}\\ = -100 \times 10^{-18}(5\times10^{-18})(150 - 5)\times 10^{-3}(10^3)/10^{-8}}\)(Note the \(\mathrm{10^3}\) in the above calculation converts concentration in \(\mathrm{mole/dm^3}\) to \(\mathrm{mole/m^3}\))
\(\mathrm{dn/dt = -7.3\times 10^{-24}\; mole/s}\)
- With C the concentration of a solute in water, measured in grams (of solute) per cubic metre (of solvent) and with M the molar mass (grams per mole) of solute:
(a) Show that \(\mathrm{C/M}\) is given by \(\mathrm{moles (of\; solute)/m^3(of \;solvent)}\)
\(\mathrm{[C]/[M] = {gm(solute)/m^3(solvent)}{moles (solute)/gm\; (solute)} = mol (solute)/m^3 (solvent)}\)
(b) Under what conditions will \(\mathrm{C/M}\) also be given by \(\mathrm{moles (of\; solute)/m^3 (of \;solution)?}\)
For very dilute solutions where the addition of solute does not appreciably change the volume
\(\mathrm{[C]/[M] = mol (solute)/m^3 (solution)}\)
(c) Under the conditions of part (b), are the molarity and molality of the solution likely to be the same?
For very dilute solution in water (as in part (b)), \(\mathrm{1\; dm^3}\) has a mass of \(\mathrm{1\; kg}\) so molarity \(\mathrm{(mol/dm^3)}\) and molality \(\mathrm{(mol/kg)}\) are the same.
- A dilute solution of sucrose is made up with concentration C. If the volume of the solution is increased 33 1/3% by the addition of pure water, the concentration will now be:
(a) (4/3)C,
(b) (2/3)C,
(c) (3/2)C,
(d) (3/4)C,
(e) (1/3)C
D
\(\mathrm{V´ = (4/3)V \\ C = Number\; of \;moles/V \\ C´ = Number\; of \;moles/V´ = Number \;of \;moles/[(4/3)V] = ¾Number\; of \;moles/V = ¾C}\)
- An experimenter finds that a solution containing \(\mathrm{15.0\; mg\; cm^{-3}}\) of a pure protein has an osmotic pressure of \(\mathrm{100\; Pa.}\) Assuming ideal behaviour, what would be the molar mass of the protein? \(\mathrm{(T = 300^\circ C)}\)
The expression for osmotic pressure (in Pa) is given by equation 11-38 in the text:
\(\mathrm{\pi = RTC/M}\)
where \(\mathrm{R}\) is the gas constant \(\mathrm{(8.3\; J/K\; mol),}\) \(\mathrm{T}\) is the absolute temperature, \(\mathrm{C}\) is the concentration in \(\mathrm{gm/m^3}\) and \(\mathrm{M}\) is the molar mass.
\(\mathrm{15\times 10^{-3} gm/cm^3(10^6 cm^3/m^3) = 15\times 10^3\; gm/m^3}\)
\(\mathrm{M = RTC/\pi = 8.3(300)(15\times 10^3)/100 = 3.74\times 10^5 \;gm/mol}\)
- Suppose some red blood cells such as those described in the text are placed in a large volume of a solution containing 0.30 molar glycerol plus 0.15 molar NaCl. What will happen to the cell? Remember the NaCl will not cross but the glycerol will.
What is the osmolarity of 0.15 molar NaCl?
0.30 Os
The NaCl ionizes into 2 species: \(\mathrm {Na^+}\) and \(\mathrm {Cl^-}\) each with an osmolarity of 0.15 Os.The initial situation is shown below.

Since water and glycerol can freely interchange across the membrane, a number of glycerol molecules will move in and an equal number of water molecules will move out until the concentration of glycerol is equalized. During this process the volume of the cell does not change. The final situation is shown below.
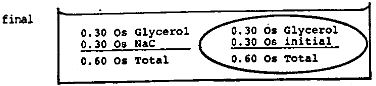
Now the osmolarity inside and outside is identical so there is no further change. The solution is isotonic.
- Some red blood cells (0.30 Os) are placed in a NaCl solution of concentration 0.27 Os.
(a) Do they swell or shrink?
Since NaCl cannot cross the membrane, water enters the cell to reduce the osmolarity to 0.27. The cell swells.
(b) By what percentage?
The change in volume is (0.3 - 0.27)/0.27 = 0.11 or 11%


