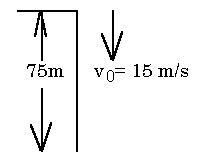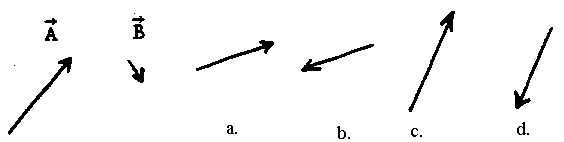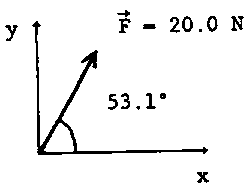Study Guide 9 - Kinematics
- A car is driven on a straight highway from town A west to town B, a distance of 10 km, in 15 minutes. What is the average speed in m/s?
What is the relation between constant speed (v), displacement (d) and time (t)?
\(\mathrm {v = d/t = 10\times 10^3\; m/(15 \times 60) s = 11\; m/s}\)
- The car in (1) is then driven 8 km north to town C and from there, 13 km back to town A.
(a) What is the overall displacement?
The displacement is defined as: final position - initial position
So in this case the displacement is zero.
(b) What is the average velocity?
Since from part a the displacement is zero then the average velocity is also zero.
- A cyclist starts down a straight road at a constant speed of 10 m/s. Ten seconds later, a 2nd cyclist starts from the same point at a constant 12 m/s. How long does it take the second to catch up with the first?
Let \(\mathrm {t}\) be the elapsed time from when the first rider starts until the second rider catches up.
\(\mathrm {Therefore\; x_1 = 10t}\)
For the second rider who starts 10 s later
\(\mathrm {x_2 = (t - 10) 12}\)
but when they meet, \(\mathrm {x_1 = x_2}\)
\(\mathrm {(t - 10) 12 = 10 t}\)\(\mathrm {t = 60 \;s}\) or \(\mathrm {50\;s}\) after the second rider starts.
- A runner's speed changes from 5.00 metres per second to 10.0 metres per second in 5.00 seconds. What is his constant acceleration?
You must use one of the Gallilean equations. In this case \(\mathrm {v = v_0 + at}\)
\(\mathrm {v = v_0 + at \\ 10 = 5 + a(5) \\ a = (10 - 5)/5 = 1 m/s^2}\)
- The graph shows the displacement s of a walking man as a function of time.
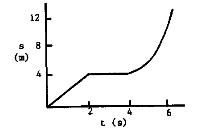
(a) What is his velocity in the first 2 seconds?
In the first 2 seconds his velocity is: Constant
So the acceleration is zero since the slope of the s vs. t curve is constant.
\(\mathrm {v = \Delta s/\Delta t = 4/2 = 2 m/s^2}\)
(b) What is his velocity in the time 2 to 4 seconds?
In the period 2 to 4 seconds his position is: Constant
Therefore his velocity is zero.
(c) What is his acceleration in the first 2 s?
Is the velocity changing in the first 2 seconds? No
The velocity is not changing; it is constant at 2 m/s, so a = 0
(d) What is his acceleration in the time 2 to 4 s?
Is the velocity changing in the period 2 to 4 seconds? No
The velocity is not changing; it is constant at a value of \(\mathrm {0\; m/s,}\) so \(\mathrm {a = 0}\)
(e) Is he accelerating in the last two seconds?
Is the velocity changing in the period 4 to 6 seconds? Yes
The velocity is the slope of the s vs. t curve, i.e., \(\mathrm {v = ds/dt.}\) This slope is clearly changing in the period 4 to 6 seconds, so the acceleration is non-zero.
- A motorist traveling at 25 m/s passes a police car traveling at 10 m/s. The motorist does not change speed. The police car accelerates at 10 m/s2 at the instant it is passed. How long does it take to catch up with the speeder?
\(\mathrm {x_m = v_mt = 25t \\ x_p = v_{0_p}t + ½(a)t^2 = 10t + ½(10)t^2 \\ but\; x_m = x_p \\ 25t = 10t + ½(10)t^2 \\ t = 3 \;s}\)
- Repeat Example 7-4 but let the ball be thrown down with an initial speed of 15 m/s. How long now to reach the bottom of the cliff?
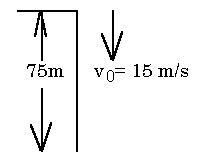
\(\mathrm {x = v_0t + ½at^2 \\ 75 = 15t + (9.8/2)t^2 \\ 4.9t^2 + 15t - 75 = 0 \\ t = -(15/9.8) ± (1/9.8)[15^2 + 4(4.9)(75)]^{½} \\ = (1/9.8)(-15 ± 41.2) Choose\; t\; positive \\ t = 26.2/9.8 = 2.67\; s}\)
- An object falls past a window 2.0 m high. If the downward speed at the top of the window is 4.0 m/s, what is it at the bottom?
\(\mathrm {v^2 = v_{0}\;^2 + 2ax = 4^2 + 2(9.8)2 = 55.2 \\ v = 7.4 \;m/s}\)
- (a)
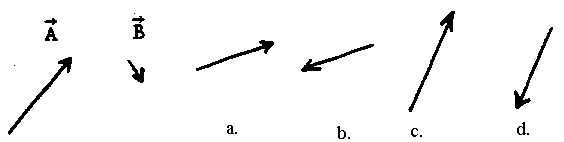
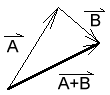
Which of the above could represent the vector sum of A + B?
a. is the correct answer
If you have difficulty with the addition of vectors you are strongly urged to use the Vector tutorial.
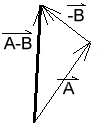
(b.) Which could represent A - B?
c. is the answer
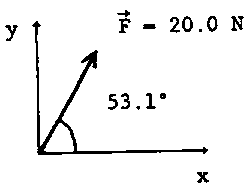
(a) What is the x component of F?
In the standard x, y coordinate system the x component over the hypotinuse is given by the cos of 53.1
\(\mathrm {So\; F_x = F \cos \;53.1^\circ = 20 \times 0.60 = 12 \;N.}\)
(b) What is the y component of F?
It follows that the y component is given by the sin of 53.1.
\(\mathrm {F_y = F \sin\; 53.1^\circ = 20 \times 0.80 = 16 \;N}\)
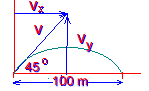
- The distance from centre field to home plate is 100 m. Assuming that the ball is thrown at an inclination of 45º with the horizontal, with what speed must the ball leave the fielder's hand if it is to reach home plate? To begin consider the following:
What forces act on the ball in the x-direction after it is released?
What forces acts on the ball in the y-direction?
What is the velocity in the x-direction?
What is the initial velocity in the y-direction?
What forces act on the ball in the x-direction after it is released?
There is no force on the ball in the x-direction. Therefore the motion of the ball in the x-direction is motion at constant velocity \(\mathrm {(a_x = 0).}\)
What forces acts on the ball in the y-direction?
The force of gravity acts in the y-direction so the motion in the y-direction is motion at constant acceleration
with \(\mathrm {a_y = -g.}\)
What is the velocity in the x-direction?
\(\mathrm {The\; velocity\; in\; the\; x-direction\; is\; +v \cos \;45^\circ}\)
What is the initial velocity in the y-direction?
\(\mathrm {The\; initial \;velocity \;of \;the \;ball\; in \;the\; y-direction\; is\; v \sin \; 45^\circ}\)
We can now proceed to solve the problem:
X-Motion Y-Motion at constant velocity
\(\mathrm {a_x = 0\; and\; v_{0x} = v \cos \;45 \\ s_x = v_xt \\ t = 100/(v \cos \;45)}\)
Use this in the right-hand column.at constant acceleration
\(\mathrm {a_y = -g \;and\; v_{0y} = v\; \sin \;45 \\ s_y = v_{0y} + ½a_yt^2}\)What is the displacement in the y-direction at the end of time t?
(a) 100 m
(b) 2 X the height of the path
(c) 0X-Motion Y-Motion at constant velocity
\(\mathrm {a_x = 0\; and\; v_{0x} = v \cos \;45 \\ s_x = v_xt \\ t = 100/(v \cos \;45)}\)
Use this in the right-hand column.at constant acceleration
\(\mathrm {a_y = -g \;and\; v_{0y} = v\; \sin \;45 \\ s_y = v_{0y} + ½a_yt^2 \\ 0 = v \; \sin \; 45 \; t + ½(-g)t^2}\)
Using t = 100/v cos 45 from the left-hand column:
\(\mathrm{0 = (v\; \sin \;45)(100/v\; \cos \;45) - (g/2)(100/v\; \cos \;45)^2 \\ 0 = 100 - 9.8 \times 10^4/v^2 \\ v^2 = 9.8 \times 10^2 \\ v = 31.3 \;m/s}\)
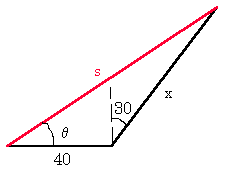
- An object travels 40.0m east at 10.0 m/s, then without changing speed, it turns 30.0 east of north. It travels in this direction for 10.0 seconds while undergoing a constant acceleration to a final speed of 20.0 m/s. What is its total displacement?
\(\mathrm{v = v_0 + at \\ 20 = 10 + a(10) \\ a = 10/10 = 1\; m/s^2}\)
\(\mathrm {x = v_0t + ½at^2 = 10(10) + ½(1)10^2 = 150 \;m}\)
\(\mathrm {s_x = 40 + 150 \sin\;30 = 40 + 75 = 115 \;m}\)
\(\mathrm {s_y = 150 \; \cos \;30 = 130 \;m}\)
\(\mathrm {s = (115^2 + 1302)½ = 173 \;m}\)
\(\mathrm {\theta = \tan^{-1} (130/115) = 48.5\; N \;of \;E}\)
- A motor boat can run at \(\mathrm {10.0 \;m\; s^{-1}}\) in still water.
(a) In what direction must the motor boat be pointed to directly cross a river flowing at \(\mathrm {3.00\; m\; s^{-1}?}\)
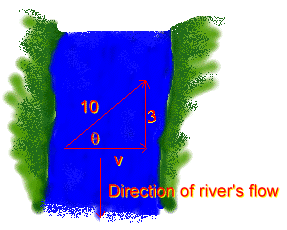
\(\mathrm {\theta = \sin^{-1}(3/10) = \sin^{-1}0.3 = 17.5^\circ}\)
(b) What is the velocity of the motor boat directly across?
The motorboat must travel across the river with speed v and also upstream at 3 m/s to counter the flow of the river. Since the boat's speed is 10 m/s then:
\(\mathrm{ 10^2 = v^2 + 3^2 \\ V^2 = 100 - 9 \\ V = 9.54\; m/s}\)
- You are drifting north in a balloon at 20 km/hr. A bird flies past you and to you it is travelling at 15 km/hr due east. What bird velocity would an observer on the ground see?
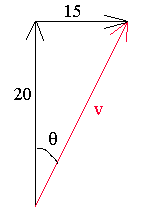
\(\mathrm {v = (20^2 + 15^2)^{1/2} = 25\; km/hr}\)
\(\mathrm{\theta = \tan^{-1} (15/20) = 37 \;degrees\; E\; of \;N}\)
- These problems will not always have the two vectors at right angles. Try this one:
City B lies 500 km from city A in a direction 30.0º east of north. An airplane is required to travel from A to B in 2.00 hr.
(a) If no wind is blowing, in what direction and with what speed must the airplane fly?
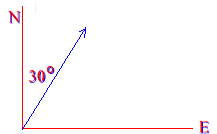
The airplane must fly 30º E of N at a speed of 500/2 = 250 km/hr.
(b) A wind is blowing from a direction 120º west of north with a speed 60.0 km hr-1. With what speed and in what direction must the airplane fly? (Hint: a good diagram is essential. Which velocity vector is the resultant vector?)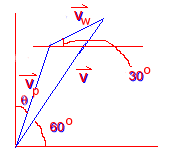
From the drawing we can see that the resultant velocity of the plane, \(\mathrm {v,}\) will be the vector sum of the velocity of the plane in still air, \(\mathrm {v_p,}\) plus the velocity of the air itself, \(\mathrm {v_w,}\) (i.e., the wind speed).
Therefore: \(\mathrm {v = v_p + v_w}\)But this means that the x and y components also add individually. In addition, the magnitude of the v vector must be 250 km/hr (see part (a)) and the magnitude of the \(\mathrm {v_w}\) vector is 60 km/hr.
First evaluate the x components:
\(\mathrm {v_x = v_{px} + v_{wx} \\ 250\; \cos \;60 = v_{px} + 60\; \cos\; 30 \\ v_{px} = 73\; km/hr}\)Now evaluate the y components:
\(\mathrm {v_y = v_{py} + v_{wy} \\ 250\; \sin \;60 = v_{py} + 60\; \sin \;30 \\ v_{py} = 187\; km/hr}\)\(\mathrm {V_p = ({v_{px}}^2 + {v_{py}}^2)½ = 200\; km/hr}\)
\(\mathrm {\theta = \tan^{-1}(73/187) = \tan^{-1}0.39 = 21.4^\circ \; E\; of\; N.}\)