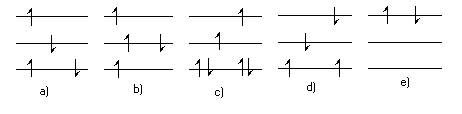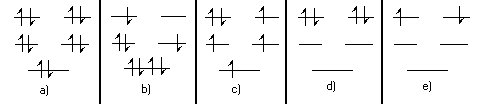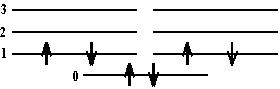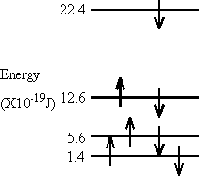Study Guide 5 - Light Absorption by II-Electrons in Biological Molecules
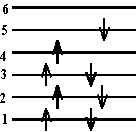
- Which of the following \(\mathrm {\pi-electron}\) configurations are possible in energy levels of a linear molecule, a, b, c, d or e?
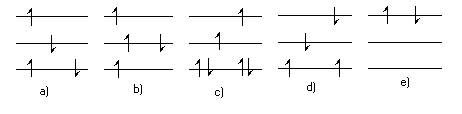
a, b and e are possible configurations. The only criterion is whether or not the Pauli Exclusion Principle is violated. Every electron must have a unique set of quantum numbers n, s. In terms of the drawing each electron must have a unique level and spin arrow.
- Which of the following \(\mathrm {\pi-electron}\) configurations are possible in energy levels of a circular molecule?
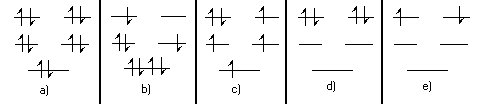
a, c, d and e are possible configurations. The only criterion is whether or not the Pauli Exclusion Principle is violated. Every electron must have a unique set of quantum numbers n, s. In terms of the drawing each electron must have a unique level and spin arrow.
- What is the energy of the lowest completely empty \(\mathrm {\pi -electronic}\) level in the 1st excited state of 1, 3, 5, 7 - octatetraene? Assume carbon-carbon bond length to be 0.15 nm.
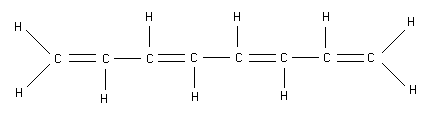
First we must determine the electron configuration in the ground state. There are \(\mathrm {8 \pi-bonded}\) Cs so there are \(\mathrm {8 \pi - electrons}\). These are distributed over the electronic levels as follows:
The first excited state of this configuration is:
So the n value of the lowest completely empty level of the 1st excited state is 6.
\(\mathrm {The\; length\; of\; the\; molecule = 7 \times 0.15 = 1.05\; nm}\)
The energy is given by:
\(\mathrm {E = \frac{n^2h^2}{8ml^2}}\)\(\mathrm {E = 6^2(6.63 \times10^{-34})^2/8(9.11 \times 10^{-31})(1.05 \times 10^{-9})^2 \\ = 2.0 \times 10^{-18} \; J}\)
- What is the energy of the highest filled p-electronic level in the ground state of benzene? (C-C bond length = 0.15 nm.) Note that in this problem the length of the circumference = bond length X number of bonds. In all ring systems such as the porphyrins (see p46 in the text) the number of bonds will equal the number of atoms in the circle, which is also equal to the number of p electrons.
We must first determine the electronic configuration of the ground state. In this case there are 6 electrons.
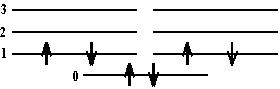
The highest filled level is that for which n = 1
The circumference, L, of the circle is given by:
\(\mathrm {L = 6 \times 0.15 \;nm = 0.75 \;nm}\)
The energy for a circular molecule is:
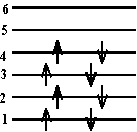
\(\mathrm {E = n ^2h^2/2mL^2 \\ E = 1^2(6.63 \times10^{-34})^2 / 2(9.11 \times 10^{-31})(0.75 \times 10^{-9})^2 \\ = 4.3 \times 10^{-19} \; J}\) - (a) The \(\mathrm {\pi-electronic}\) energy level diagram of a molecule is shown at the left. If a photon of wavelength 118.4 nm is absorbed by the molecule what is the resultant energy level diagram?
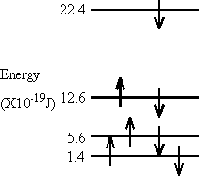
(b) Would a photon with \(\mathrm {\lambda = 473\; nm}\) be absorbed?
(a) What energy difference does 118.4 nm represent?
\(\mathrm {\Delta E = hc/\lambda = (<6.63 \times 10^{-34})(3.0\times 108/118.4 \times 10^{-9} ) \\ = 16.8 \times 10^{-19} \; J}\)Now can you find such an energy difference in the diagram?
It is between the 2nd and 4th levels (22.4 - 5.6 = 16.8). So one of the 2 electrons in the 2nd level will go to the 4th. Which one will it be?
(b) The energy difference is:
\(\mathrm {\Delta E = hc/\lambda = (6.63 \times 10^{-34})(3 \times 10^8/473 \times 10^{-9}) \\ = 4.2 \times 10^{-19} \; J}\)
Is there such an energy difference in the diagram?Yes! Between the 1st and 2nd levels.
Can this transition take place?
No. The 2nd level is already filled. Adding another electron would violate the Pauli Exclusion Principle.
- A molecule in which there is a sequence of conjugated double bonds 10 atoms long is observed to have a maximum absorption at 450 nm. For a similar molecule in which the conjugated sequence is only 6 atoms long, at what energy would you expect to find the maximum absorption?
We dont know what atoms are involved so assuming that the bond length is 0.15 nm is an unwarranted assumption, and is in fact unnecessary. The problem states that the molecules are similar i.e., they have the same bond length.
Bond length = b
Length of 10 atom chain = 9b
Length of 6 atom chain = 5bThe ground state configuration of the 10 electrons is:
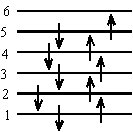
Therefore the lowest energy transition is from n = 5 to n = 6.
\(\mathrm {\Delta E _{10} = \frac{hc}{\lambda _{10}} = \frac{(6^2 - 5^2)h^2}{8m\ell ^2}= \frac{(6^2 - 5^2)h^2}{8m(9b)^2}}\)The ground state configuration of the 6 electrons is:
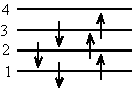
Therefore the lowest energy transition is from n = 3 to n = 4.
\(\mathrm {\Delta E_6 = \frac{hc}{\lambda_6} = \frac{(4^2-3^2)h^2}{8m\ell^2}= \frac{(4^2 - 3^2)h^2}{8m(5b)^2}}\)\(\mathrm {Divide\; \Delta E_6\; by\; \Delta E_{10}}\)
\(\mathrm{\frac{\Delta E_6}{\Delta E_{10}}= \frac{hc}{\lambda _6} \frac{\lambda _{10}}{hc} = \frac{(4^2 - 3^2)}{5^2}\frac{9^2}{(6^2 - 5^2)} = 2.06 \\ \Delta E_6 = 2.06\Delta E_{10} \\ = 2.06 \frac{hc}{\lambda _{10}}= 2.06 \frac{(6.63 \times 10^{-34})(3 \times 10^8)}{450 \times 10^{-9}} \\ = 9.1 \times 10^{-19 \; J}}\)