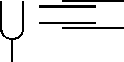Study Guide 2 - Acoustics
- Sketch the lowest frequency resonance possible in each of the following:
(a) The tube is open at each end. What must be at each of these ends?

(b) The tube is closed at the right end and open at the left. What is at each end?

Option Left Right (1) node node (2) node antinode (3) antinode node (4) antinode antinode
(c) The tube is closed at each end. What must be at each of these ends?

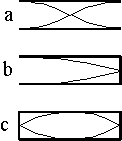
(a) This is a Displacement Antinode, because the molecules are free to move there. Since the minimum number of nodes possible is 1, then the standing wave pattern must be:

NOTE: This is NOT a displacement node because the molecules are free to move at these positions. At a displacement node there is no motion. In this case there must be displacement antinodes at each end.
(b) The tube is closed at the right end and open at the left. What is at each end?- (1) node - node: No: Molecules are not free to move at the right end but are free to move at the left end. There must be a displacement node at the right and a displacement antinode at the left.
- (2) node - antinode: No: Molecules are not free to move at the right end but are free to move at the left end. There must be a displacement node at the right and a displacement antinode at the left.
- (3) antinode - node: Yes. The molecules are free to move at the left end (displacement antinode) and cannot move at the right end (displacement node). The standing wave pattern must be:

- (4) antinode - antinode: No: Molecules are not free to move at the right end but are free to move at the left end. There must be a displacement node at the right and a displacement antinode at the left.
(c) This is a Displacement Node, because the molecules are not free to move there so there must be a displacement node at each end. The minimum number of antinodes between 2 nodes is 1 so the standing wave pattern must be:
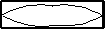
NOTE: This is NOT a displacement antinode. The molecules are not free to move. At a displacement antinode the molecules must be free to move. There must be a displacement node at each end. - Sketch the next highest frequency in each of the above cases.
The next highest frequency will have one more node in each case so the standing wave patterns will be:
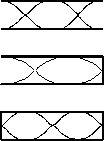
- If the velocity of the sound in the air in the tubes is 340 m/s, and each of the above tubes is 1.00 m long, find the resonance frequency in each case a, b, and c in problems 1 and 2.
Let us first look at the cases in problem 1. Since the length of the tube is 1 m:
Examples \(\lambda\) \(\mathrm { f = v/\lambda = 340/\lambda}\) a \(\mathrm { 2\;m}\) \(\mathrm {340/2 = 170 \;Hz}\) b \(\mathrm { 4\;m}\) \(\mathrm {340/4 = 85 \;Hz}\) c \(\mathrm { 2\;m}\) \(\mathrm {340/2 = 170 \;Hz}\) - A tuning fork is set up near the end of an air filled tube of variable length as shown. By changing the length, various positions of maximum loudness (resonances) can be found. The difference in tube length between adjacent maxima is found to be 10.0 cm.
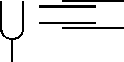
(a) What is the wavelength in air of this sound?
(b) What is the frequency of the tuning fork \(\mathrm {(v = 340 m/s)}\)?
(c) Would closing the right hand end of the tube change the 10.0 cm measurement?
(a) The distance between two adjacent resonances (nodes) is 1/2 wavelength so
\(\mathrm {\lambda =20 \;cm = 0.20 \;m}\)
(b) \(\mathrm {f = v/\lambda = 340/0.20 = 1.70\times 10^3 \;Hz}\)
(c) No: It would just shift the pattern by 1/4 \(\lambda\) making the right end a node instead of an antinode. - While tuning a piano, the tuner observes 5 beats per second when he sounds the second harmonic (512 Hz) of the middle C string along with the upper C string. What are the possibile frequencies of the upper C string?
Beats occur at the differences of the two frequencies involved. However we don't know if the upper C is at a higher or a lower frequency than 512 Hz. So the possibilities are:
512 + 5 = 517 Hz
512 - 5 = 507 Hz - Obtain the following logarithms using your calculator:
(a) \(\log \;2.00\)
(b) \(\log \;10.0\)
(c) \(\log \;1.13\)
(d) \(\log\; (1.40\times 10^6)\)
(e) \(\log \;0.000670\)
(f) \(\log\; 9.40\times10^{-6}\)
(g) \(\log \;94.0\times10^{-7}\)
(a) \(\mathrm {\log\; 2.00 = 0.301}\)
(b) \(\mathrm {\log \;10 = 1}\)
(c) \(\mathrm {\log\; 1.13 = 0.053}\)
(d) \(\mathrm {\log \;(1.40\times 10^6) = 6.146}\)
You should notice that it is also
\(\mathrm {6 + \log\; 1.40 = 6 + 0.146 = 6.146}\)
(e) \(\mathrm {\log \;(0.000670) = -3.174}\)
You should notice that it is also
\(\mathrm {-4 + \log \; 6.70 = -4 + 0.826 = -3.174}\)
(f) \(\mathrm {\log \;(9.40\times10^{-6}) = -5.027}\)
You should also notice that it is
\(\mathrm {-6 + \log \;9.40 = -6 + 0.973 = -5.027}\)
(g) \(\mathrm {\log \;(94.0\times10^{-7}) = \log\; (9.40\times 10^{-6})}\)
so the answer is the same as for Question 6. (f) above
Note: The number of significant figures in a logarithm is only the number of places after the decimal point since the integer part only gives the power of 10. All the numbers in the question (except (b)) are given to 3 figures and so the answers are given to 3 figures. - Using your calculator obtain the antilogarithms of the following:
(a) 0.724
(b) 1.724
(c) -0.689
(d) -6.89
(e) -0.0100
(a) \(\mathrm {antilog \;(0.724) = 5.30}\)
(b) \(\mathrm {antilog\;(1.724) = 53.0}\)
(c) \(\mathrm {antilog\; (-0.689) = 0.205}\)
(d) \(\mathrm {antilog\; (-6.89) = 1.3\times 10^{-7}}\)
(e) \(\mathrm {antilog\; (-0.0100) = 0.977}\)Note: The only significant figures in a logarithm are those after the decimal piont. The integer part just gives the power of 10. In the following there are 3 significant figures in (a), (b), (c) and (e); (d) has 2 sig. fig. This must be preserved in the answer.
- Evaluate the following:
(a) \(4.00^{0.360}\)
(b) \((7.10)^{\log \;3.20}\)
(c) \((\log 2.40)^{\log \;0.930}\)
Powers like this can be solved directly on most calculators by using the \(\mathrm {y^x}\) key.
If you don't have a \(\mathrm {y^x}\) key, they can be solved by taking logarithms:(a) \(\mathrm {\log \;(4.00^{0.360}) = 0.360 \log \;4.00 = 0.360\times 0.602 = 0.2167}\)
\(\mathrm {antilog \;(0.2167) = 1.65}\)(b) \(\mathrm {(7.10)^{\log\;3.20} = 7.10^{0.505}}\)
\(\mathrm {\log\; (7.10^{0.505}) = 0.505 \log\; 7.10 = 0.505\times 0.851 = 0.4299}\)
\(\mathrm {antilog\; (0.4299) = 2.69}\)(c) \(\mathrm {(\log \;2.40)^{\log 0.930} = 0.380^{-0.0315}}\)
\(\mathrm {\log \;(0.380^{-0.0315}) = -0.0315\; \log \;0.380 = -0.0315(-0.4202) = 0.01324}\)
\(\mathrm {antilog (0.01324) = 1.03}\) - Find z in each of the following:
(a) \(\mathrm {42.0^{(z - 3)} = 7.00}\)
(b) \(\mathrm {4.0(8.0)^z = 7.0(3.0)^{(z - 1)}}\)
These equations can only be solved by taking logarithms of both sides of the equation.
(a) \(\mathrm {42.0^{(z - 3)} = 7.00}\)
\(\mathrm {\log [42.0^{(z-3)} ] = log \;7.00}\)
\(\mathrm {(z - 3) 1.623 = 0.845}\)
\(\mathrm {z - 3 = 0.521}\)
\(\mathrm {z = 3.52 (3 \;sig. \;fig)}\)
(b) \(\mathrm {4.0(8.0)^z = 7.0(3.0)^{(z - 1)}}\)
\(\mathrm {\log \;4.0 + z\; \log \;8.0 = \log \;7.0 + (z - 1) \log \;3.0}\)
\(\mathrm {0.602 + 0.903\; z = 0.845 + 0.477 (z - 1)}\)
\(\mathrm {0.602 + 0.903 \;z = 0.845 + 0.477 \;z - 0.477}\)
\(\mathrm{0.426 \;z = -0.234}\)
\(\mathrm {z = -0.55 \;(2\; sig. \;fig)}\)
- Simplify:
\(\frac{\log(ab^2) + \log\left( \frac{1}{a^2b}\right)}{4\log\left[\left(\frac{1}{a^3}\right)(b)\left(\frac{1}{a^2}\right)\right]}\)
It will help to simplify the numerator and denominator separately and then take the ratio.
Simplify numerator
\(\mathrm {\log (ab^2) + log (1/a^2b)}\)
\(\mathrm {= \log (ab^2) + log (a^{-2}b^{-1})}\)
\(\mathrm {= \log \;a + 2\; \log\; b -2 \; \log \;a - \log \;b}\)
\(\mathrm {= -\log \;a + \log \;b}\)
\(\mathrm {= \log \;(b/a)}\)Simplify denominator
\(\mathrm {4 \; \log [(1/a^3)(b)(1/a^{-2})]}\)
\(\mathrm {= 4\; log\; (a^{-1} b) = 4 \;log\; (b/a)}\)\(\mathrm {Ratio = [\log\; (b/a)]/[4\; \log\;(b/a)] = 1/4}\)
- \(\mathrm {\log \;(a + b) = ?}\) Which of the following is correct?
(a) \(\mathrm {(\log\; a)\cdot(\log \;b)}\)
(b) \(\mathrm {\log\; a + \log\; b}\)
(c) \(\mathrm {a + \log\; b}\)
(d) \(\mathrm{10a + b}\)
(e) none of the above
e - None of the above!
- Find the intensity level of sound with the following intensities.
(a) \(\mathrm {6.84\times10^{-6} W/m^2}\)
(b) \(\mathrm {45.6\times 10^{-14} W/m^2}\)
(a) \(\mathrm {6.84\times10^{-6} W/m^2}\)
\(\mathrm {IL = 10\;\log \;(I/I_0)}\)
\(\mathrm {where\; I_0 = 10^{-12} W/m^2}\)
\(\mathrm {IL = 10 \; \log (6.84\times 10^{-6}/10^{-12})}\)
\(\mathrm {= 10 \; \log \;6.84\times 10^6}\)
\(\mathrm {= 10 (6.835) = 68.4 \;db}\)
(b) \(\mathrm {45.6\times 10^{-14} W/m^2}\)
\(\mathrm {IL = 10 \; \log (I/I_0)}\)
\(\mathrm {where\; I_0 = 10^{-12} \;W/m^2}\)
\(\mathrm {IL = 10\; \log \;(45.6\times 10^{-14}/10^{-12})}\)
\(\mathrm{= 10 \; \log \; 45.6\times 10^{-2}}\)
\(\mathrm {= 10 \;(-0.341) = -3.41\; db}\) - Find the intensity corresponding to the following:
(a) \(\mathrm {-18.0 \;db}\)
(b) \(\mathrm {118 \;db}\)
(a) \(\mathrm {-18.0 \;db}\)
\(\mathrm {IL = 10\; \log\; (I/I_0)}\)
\(\mathrm {where\; I_0 = 10^{-12} \;W/m^2}\)
\(\mathrm {-18.0 = 10\; \log\; (I/10^{-12})}\)
\(\mathrm {\log \;(I/10^{-12}) = -1.8}\)
\(\mathrm {I/10^{-12} = 0.0158 \;I = 1.58\times 10^{-14} \;W/m^2}\)
(b) \(\mathrm {118 \;db}\)
\(\mathrm {IL = 10\; \log\; (I/I_0)}\)
\(\mathrm {where\; I_0 = 10^{-12}\; W/m^2}\)
\(\mathrm {118 = 10\; \log \;(I/10^{-12})}\)
\(\mathrm {\log\; (I/10^{-12}) = 11.8}\)
\(\mathrm {I/10^{-12} = 6.3\times 10^{11}}\)
\(\mathrm {I = 0.63 \;W/m^2}\) - Two sounds differ in intensity level by 105 db. What is the ratio of the intensities of the sounds?
\(\mathrm {IL_1 = 10 \; \log \; (I_1/I_0)}\)
\(\mathrm {IL_2 = 10\; \log\; (I_2/I_0)}\)
\(\mathrm {IL_1 - IL_2 = 1\;0\ log \; [(I_1/I_0) - (I_2/I_0)]}\)
\(\mathrm {= 10\; \log \;(I_1/I_2)\; (Remember\; the \;difference\; of\; logs\; is \;the\; log \;of\; the \;quotient)}\)
\(\mathrm {105 = 10\; \log\; (I_1/I_2)}\)
\(\mathrm {\log \;(I_1/I_2) = 10.5}\)
\(\mathrm {(I_1/I_2) = 3.2\times 10^{10}}\) - What sound intensity level is produced when 3 identical loud speakers in a sound system are all switched on assuming that the intensity \(\mathrm {(W/m^2)}\) of each speaker alone is sufficient to produce an 80.0 db sound level. (Neglect interference effects.)
When sounds are added together what adds? Their intensity? Their intensity levels?
Their intensity.
\(\mathrm {80 = 10\; \log \;(I/10^{-12})}\)
\(\mathrm {log\; (I/10^{-12}) = 8}\)
\(\mathrm {I/10^{-12} = 1\times 10^8}\)
\(\mathrm {I = 1\times 10^{-4} \;W/m^2}\)For 3 speakers:
\(\mathrm {3I = 3\times 1 \times 10^{-4} = 3\times 10^{-4} \;W/m^2}\)
\(\mathrm {IL = 10\; \log \; (3\times 10^{-4} /10^{-12})}\)
\(\mathrm {= 10\; log\; 3\times 10^8 =10 \times 8.48 = 85 \;db}\) - If a person's hearing threshold is 0 db at 1000 Hz, which of the following is a reasonable value for the threshold at 9000 Hz? Note this is not a problem. It is a test of your knowledge of the hearing curve.
(a) -10 db
(b) 0 db
(c) 10 db
(d) 20 db
(e) 130 db
- At approximately what frequency does an average person have the best hearing?
At about 3500 Hz.
- A source of sound radiates 10.0 watts.
(a) If it is placed at the centre of a sphere 1.00 m in radius, how much power is incident on the sphere?
(b) What power is incident on one square metre of a sphere of radius 1 m?
(c) What is the intensity of the sound at a distance of one metre from the source?
(d) What energy is incident on the sphere if the source is turned on for 2.00 s?
(a) 10 watts
(b) \(\mathrm {Area\; of\; sphere = 4\pi \; r^2 = 4\pi(1)^2 = 12.6 \;m^2}\)
\(\mathrm {P/A = 10W/12.6\; m^2 = 0.796 \;W/m^2}\)
\(\mathrm {Therefore \;the\; power \;on\; 1\; m^2 \;is\; 0.796 \;W.}\)
(c) The intensity of the sound is just the power per unit area, so the answer is the answer to part (b)
(d) \(\mathrm {Energy = Power \times time = 10 \times 2 = 20\; j}\) - If the same source as in Q18 is now placed at the centre of a sphere 10.0 m in radius,
(a) how much power is incident on the sphere?
(b) what is the intensity at a distance of 10.0 m from the source?
(c) what power is incident on a 10.0 X 10.0 cm square of the sphere?
(d) If the source is turned on for 3.00 s, how much energy is incident on the square in (c)?
(a) \(\mathrm {As\; in\; Q1(a)\; P = 10 \;W}\)
(b) There are 2 ways to solve this:1. \(\mathrm {I =P/A = 10/[4\pi (10)^2] = 7.96\times10^{-3} W/m^2}\)
2. Remembering from Q18 (b) that the intensity at 1 m was \(\mathrm {0.796\; W/m^2}\) and using the inverse square law:
\(\mathrm {I =P/A = 0.796/10^2 = 7.96\times 10^{-3}\; W/m^2}\)(c) From part (b) \(\mathrm {I = 7.96\times 10^{-3} \;W/m^2}\)
\(\mathrm {Area = 0.10 \times 0.10 = 0.010 \;m^2}\)
\(\mathrm{Power = IA = 7.96\times 10^{-3} (W/m^2) \times 0.010\; m^2}\)
\(\mathrm {= 7.96\times 10^{-5} \; W}\)
(d) From part (c) , \(\mathrm {Power\; on\; square = 7.96\times 10^{-5}\; W}\)
\(\mathrm {Energy = Power \times time = 7.96\times 10^{-5} \times 3.00 = 2.39\times 10^{-4}\; j}\) - Name the parts of the ear indicated in the diagram. The inner ear is shown schematically; it is actually coiled.
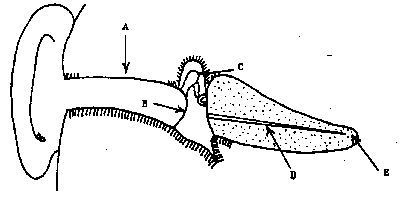
(a) Auditory Canal
(b) Tympanic Membrane
(c) Ossicles
(d) Basilar Membrane
(e) Helicotrema