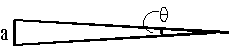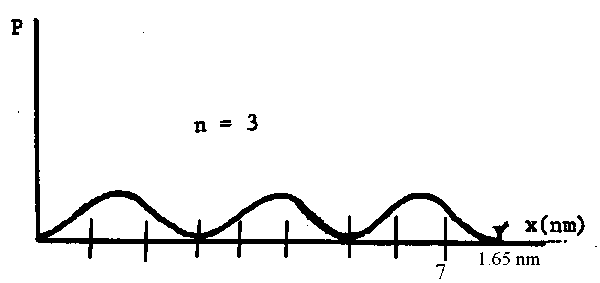Study Guide 4 - Diffraction, Electromagnetic Waves and Particle Waves
- What angle does a 25-cent piece (2.4 cm in diameter) in Hamilton suspend at Guelph (distance 50 km)?
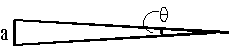
\(\mathrm {The\; relationship\; between\; a, \;r \;and\; q\; is;}\)
\(\mathrm {a = r\; \theta}\)
\(\mathrm {when\; \theta \; is\; in\; radians.}\)
\(\mathrm {q = a/r = 2.4/50\times 1000\times 100 = 4.8\times 10^{-7} \;radians}\) - The racing driver Lotta Lotus has pupil diameters of 2.00 mm and normal vision. If the night is clear, what is the maximum distance at which she can distinctly see another car's two headlights? (Assume a headlight spacing of 1.50 m and a wavelength of 550 nm.)
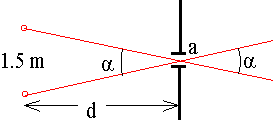
\(\mathrm {a = 1.5/d = 1.22\; \lambda/a = (1.22\times 550\times 10^{-9} )/(2\times 10 ^{(-3)})}\)
\(\mathrm {d = 4.47\times 10^3 \;m}\) - Arrange the following in order of decreasing wavelength:
red light, radio waves, infrared, X-rays, ultraviolet, blue light.
Decreasing wavelength
\(\mathrm {Radio \;waves: \lambda \sim 1 - 10 \;m}\)
\(\mathrm {Infrared: \lambda \sim 10^{-6} \; m}\)
\(\mathrm {Red\; light: \lambda \sim 8000\times 10^{-10} \; m}\)
\(\mathrm {Blue\; light: \lambda \sim 4000\times 10^{-10}\; m}\)
\(\mathrm {Ultraviolet: \lambda \sim 2000\times 10^{-10} \;m}\)
\(\mathrm {X-rays: \lambda \sim 100\times 10^{-10} \; m}\) - Radio station CJOY (Guelph) is located at 1460 on the AM band; this means that CJOY broadcasts at 1460 kHz (1.46X106 Hz).
(a) What is the wavelength of a CJOY radiowave?
What is the relationship between frequency (f), wavelength (l) and speed of light (c)?
(b) What is the energy of a CJOY photon?
What is the relationship between energy of a photon (E) and its frequency (f)?
(a) \(\mathrm {f = 1.46\times 106 \;Hz}\)
\(\mathrm {c = f\lambda \;where\; c = 3.00\times 108\; m/s}\)
\(\mathrm {Therefore\; \lambda = c/f = 3\times 108/1.46\times 106 = 205 \;m}\)
(b) \(\mathrm {f = 1.46\times 106 \;Hz}\)
\(\mathrm {E = hf \;where\; h \;is \;Planck's\; constant = 6.63\times 10^{-34} \; J.s}\)
\(\mathrm {E = (6.63\times 10^{-34})(1.46\times 10^6) = 9.68\times 10^{-28}\; J}\) - Typical X-rays have a wavelength of 0.01 nm. What is the energy of one of the X-ray photons. How many CJOY photons are required to equal the energy of one of these X-ray photons? What is the relationship between the energy of a photon (E) and its wavelength \((\lambda)\)?
\(\mathrm {E = hc/\lambda}\)
\(\mathrm {In\; this \;case\; (\lambda) = 0.10\times 10^{-9} \; m}\)
\(\mathrm {E = hc/\lambda = (6.63\times 10^{-34})(3.00\times 10^8/0.10\times 10^{-9})}\)
\(\mathrm {= 1.2\times 10^{-15}\; J}\)
\(\mathrm {The\; CJOY\; photon\; from\; Question \;4\; had\; energy\; 9.68\times 10^{-28} \; J.}\)
Number of CJOY photons required to make the energy of one X-ray photon
\(\mathrm {= 1.2\times 10^{-15}/9.68\times 10^{-28} = 2.1\times 10^{12}}\) - What must be the speed of a neutron \(\mathrm {(m = 1.67\times 10^{-27} \; kg)}\) to have the same wavelength as the X-rays in Question 5?
What is the relationship between wavelength \((\lambda)\) and speed \(\mathrm {(v)}\) for particles?
\(\mathrm {\lambda = h/mv}\)
\(\mathrm {From\; Question\; 5, \lambda = 0.10\; nm \;and \;knowing \;that \;the \;mass \;of \;the \;neutron \;is \; 1.67\times 10^{-27} \; kg}\)
\(\mathrm {\lambda = h/mv}\)
\(\mathrm {v = h/m\lambda = 6.63\times 10^{-34}/(1.67 \times 10^{-27})(0.10 \times 10^{-9})}\)
\(\mathrm {= 3970 = 4.0 \times 10^3 \;m/s}\) - An electron \(\mathrm {(m_e = 9.11 \times 10^{-31} \; kg)}\) has a kinetic energy of \(\mathrm {6.00 \times 10^{-22} \;J.}\) What is the energy of a photon which has the same wavelength as that of the electron?
First of all we need to find the wavelength of the electron. To do this we need its speed. What is the expression for the Kinetic Energy (KE) of a particle?
\(\mathrm {KE = (1/2)mv^2}\) OR \(\mathrm {KE = mv}\)
\(\mathrm {KE = (1/2)mv^2 \;is \;correct}\)
\(\mathrm {Therefore\; v^2 = 2(KE)/m \\ = 2(6.00\times10^{-22})/9.11\times 10^{-31}) = 1.3172 \times 10^9 \\ v = 3.629\times 10^4 \;m/s}\)
\(\mathrm {Now \;using \;deBroglie's \;equation: \\ \lambda = h/mv = 6.63 \times 10^{-34}/(9.11 \times 10^{-31} \times 3.629 \times 10^4) \\ = 2.005 \times 10^{-8} \; m}\)
\(\mathrm {Now\; using\; Planck's\; equation: \\ E = hc/\lambda = 6.63 \times 10^{-34} \times 3 \times 10^8/2.005\times 10^{-8} \\ = 9.92 \times 10^{-18} \; J}\)
OR a more elegant and shorter solution:
\(\mathrm {KE = (1/2)mv^2 \\ v^2 = 2KE/m \\ v = (2KE/m)^{1/2} \\ \lambda = h/mv or v = h/m\lambda \\ Therefore, h/ml = (2KE/m)^{1/2}}\)
\(\mathrm {Multiply\; both\; sides\; by\; mc; \\ hmc/m\lambda = hc/\lambda = (2KE/m)^{1/2}mc \\ E = hc/\lambda = (2Kem)^{1/2}c \\ = [2(6.00 \times 10^{-22})(9.11 \times 10^{-31})]^{1/2}3.0 \times 10^8 \\ = 9.92 \times 10^{-18} \; J\; as\; before.}\)
Notice that the value of Planck's constant h was not needed.
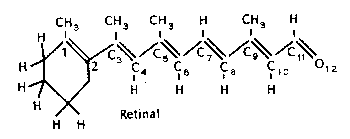
(a) What is the maximum probability density of an n = 3 electron in retinal? In the figure the oxygen atom adds one p-electron to the p-system, just as a carbon atom.
What is the equation for the Probability density?
\(\mathrm {\Psi = \sqrt \frac{2}{\ell} \sin \frac {n\pi x}{\ell}}\) OR \(\mathrm {\Psi ^ 2 = \frac {2}{\ell} \; \sin ^2 \frac{n\pi x}{\ell}}\)
The probability density is:
\(\mathrm {\Psi ^2 = \frac {2}{\ell} \; \sin ^2 \frac{n\pi x}{\ell}}\)
\(\mathrm {The\; value\; of\; \Psi^2 \; is\; a\; maximum\; when\; \sin n\pi x/\ell \;is\; a\; maximum.\\\;The\; maximum\; of\; any\; sine \;is\; 1, so: \Psi^2\;_{max} = 2/\ell}\)
What is length of the retinal \(\mathrm {\pi-chain,}\) which has 12 atoms?
\(\mathrm {11\times 0.15 = 1.65 \;nm}\)
\(\mathrm {So\; the\; maximum\; value\; of\; \Psi^2\; is:\Psi^2 = 2/\ell = 2/1.65 = 1.21 \;nm^{-1}}\)
(b) At what position in the molecule does this maximum occur?
If n = 3 then there are 3 maxima in the graph of \(\mathrm {\Psi^2.}\) It looks like this:
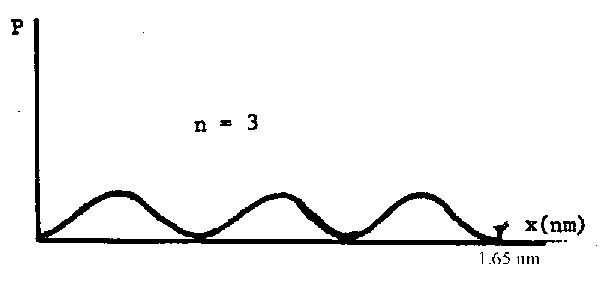
The maxima are at (1/6)l, (1/2)l and (5/6)l where l = 1.65 nm
(c) Near what location in the molecule does an n = 3 electron spend the least amount of time?
The graph of \(\mathrm {\Psi^2}\) vs \(\ell \) looks like this:
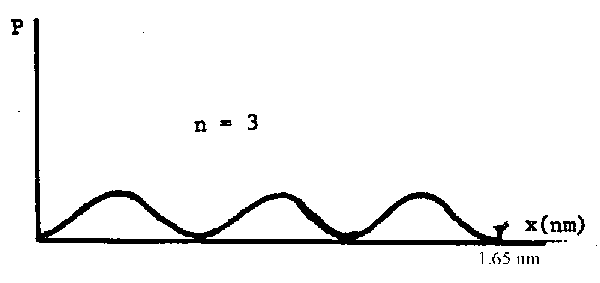
The probability is zero at 0, \((1/3)\ell\), \((2/3)\ell\) and \(\ell\)
(d) What is the probability of finding an n = 3 electron in a region of length 0.0050 nm centred at the tenth carbon atom?
What is the distance from the end to the 10th atom?
9b where b is the bond length.
Now find the probability density (probability per unit length) at the position of the 10th atom.
\(\mathrm {\Psi^2 = \frac{2}{\ell} \sin^2 \frac{n \pi x}{\ell}}\)
\(\mathrm {Where\; \ell = 11b, n = 3 \; and \; x = 9b}\)
\(\mathrm {\Psi^2 = [2/(11 \times 0.15)] \sin^2[3\pi (9b)/(11b)] \\ = 1.21 \sin^2(27/11) \pi \; {angle\; in \; radians} \\ = 1.21 \sin^2(27/11)180^\circ \;{angle \; in \; degrees} \\ = 1.21 \sin^2 442^\circ \\ = 1.21 \times (0.99)^2 = 1.19 \; nm^{-1}} \\\)
Probability of finding the electron in a distance 0.0050 nm centered at the 10th atom
\(\mathrm {= 1.19\; nm^{-1} \times 0.0050 \;nm = 5.9\times 10^{-3}}\)
(e) What is the wavelength of the electron in (d)?
Look at the \(\Psi^2\) graph:
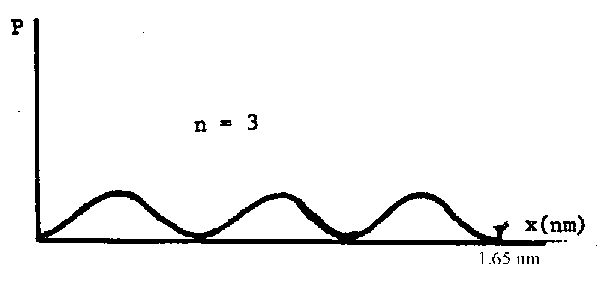
There is clearly 1½ wavelengths in the length of the chain which is 1.65 nm long. Therefore the electron wavelength is (2/3) 1.65 = 1.10 nm.
(f) Consider a chromophore having ten carbon atoms in its conjugated p-system. What is the probability of finding an n = 3 p-electron somewhere between carbon 1 and carbon 7?The probability distribution for this chain is shown below with the position of the 10 atoms indicated.
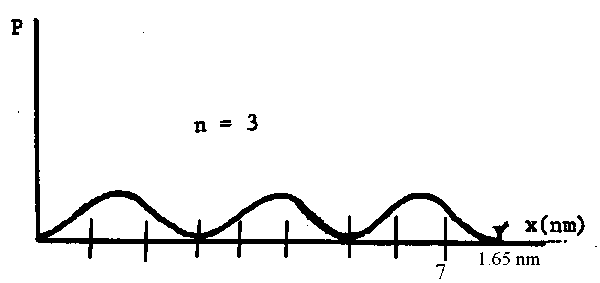
The probability of finding the electron somewhere on the chain is 1. This is the total area under the graph.
Clearly the probability of finding the electron somewhere between atoms 1 and 7 is 2/3 of this i.e., \(\mathrm {(2/3)\times1 = 2/3.}\)