Study Guide 12 - Elasticity and Scaling
- A mass is hung on a tendon of length \(\mathrm {20 \;cm}\) and cross-sectional area \(\mathrm {2 \;mm^2.}\) The tendon streches \(\mathrm {1 cm.}\) If Young's modulus for the tendon is \(\mathrm {2\times 10^7 \;N \;m^{-2},}\) what mass was hung on the tendon?
What is the relationship between "stress", "strain" and "Young's modulus"?
stress = Y strain
\(\mathrm {F/A = Y(\Delta\; L/L) \\ m(9.8)/2\times 10^{-6} = 2\times 10^7(1/20)}\)
Notice: On the right hand side of the above equation the lengths have been entered in cm. This is OK since \(\mathrm {\Delta L/L}\) is a ratio and any length units can be used so long as they are the same on top and bottom. On the left hand side however, proper units must be used since Y is in proper units)\(\mathrm {m = 0.20\; kg}\)
- The shear modulus of aluminum is \(\mathrm {2.62\times 10^{10} N\;m^{-2},}\) of copper \(\mathrm {4.83\times 10^{10} N\; m^{-2}}\) and of glass \(\mathrm {2.0\times106{10} N\; m^{-2}.}\) If you have identical pieces (i.e., same dimensions) of aluminum, copper and glass, which one would twist most easily?
The relationship between applied torque, \(\tau\), and twist angle, \(\mathrm {\theta,}\) is:
\(\mathrm { \tau = \frac{\pi Gr^4 \theta}{2 \ell}}\)
where r is the radius of the sample of length \(\ell\) and G is the shear modulus.
Clearly for a given \(\theta\) the smallest torque is for the sample with the smallest G.
Substance \(\mathrm {G(N/m^2)}\) Al \(\mathrm {2.62\times 10^{10}}\) Cu \(\mathrm {4.83\times 10^{10}}\) Glass \(\mathrm {2.0\times10^{10}}\)
The easiest to twist is glass.
- Two solid circular cylinders made of the same substance \(\mathrm {(shear\;modulus = 1.0\times10^{10}\; N\; m^{-2})}\) and of the same length are subjected to torques which twist both cylinders through a twist angle of 1º. The torques are in the ratio of 1 to 9.
(a) What is the ratio of the cross sectional areas of the cylinders?
The relationship between applied torque, \(\mathrm {\tau,}\) and twist angle, \(\mathrm {\theta,}\) is:
\(\mathrm{\tau = \frac{\pi Gr^4 \theta}{2 \ell}}\)
where r is the radius of the sample of length \(\ell\) and G is the shear modulus.
For two cylinders that differ only in radius for a given twist angle:
\(\mathrm {\tau _1/\tau_2 = (r_1/r_2)^4 = (A_1/A_2)^2}\)
where A is the cross-sectional area
\(\mathrm {\tau _1/\tau_2 = 1/9 = (A_1/A_2)^2}\)
Therefore \(\mathrm{A_1/A_2 = 1/3}\)
(b) What is the ratio of the radii of the cylinders?
As seen in part (a):
\(\mathrm {A_1/A_2 = 1/3}\)
Therefore \(\mathrm {r_1/r_2 = (1/3)^½}\)
- Which of the following graphs correctly illustrates the relation between torque \(\tau\) and radius r of a solid circular cylinder of a fixed length for a given angle of twist?
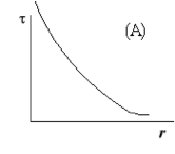
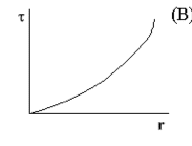
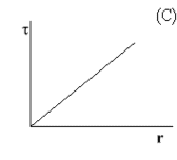
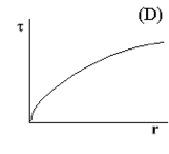
The relationship between applied torque, \(\mathrm {\tau,}\) and twist angle, \(\mathrm {\theta ,}\) is:
\(\mathrm{\tau = \frac{\pi Gr^4 \theta}{2 \ell}}\)
where r is the radius of the sample of length \(\ell\) and G is the shear modulus.
For all other things constant:
\(\mathrm {\tau \sim r^4}\)
Therefore graph B is correct.
- Explain in one sentence what is meant by the statement: "A certain object is elastic with respect to shear stresses".
After an object has been twisted by a shear stress it returns to its original state when the shear stress is removed.
- A taxidermist has to mount two similarly shaped fish, of mass 8.0 and 27 kg. How many times longer than the short one is the long one?
The mass of an object is proportional to the volume of the object.
\(\mathrm {M \sim V}\)
The volume is proportional to what power of the linear dimension?\(\mathrm {V \sim L^3 \\ Therefore\; M \sim L^3}\)
\(\mathrm {M_1/M2 = (L_1/L_2)^3 = 27/8 \\ L_1/L_2 = 3/2 = 1.5}\)
- Two steel spheres are to be painted. One has 8 times the mass of the other. What is the ratio of the amount of paint required to cover the large one to the amount required to cover the small one? Note that since the spheres have the same density, the larger one must be 8 times the volume of the smaller one. The paint layer would have the same thickness on both spheres.
The amount of paint is proportional to the surface area of the spheres.
If the ratio of the masses (volumes) is 8, what is the ratio of the surface areas?
\(\mathrm {V \sim L^3 \sim 2^3 = 8 \\ A \sim L^2 \sim 2^2 = 4}\)
So 4 times as much paint is needed.
- Suppose one developed a "super-cow" having a body mass (excluding the contribution of the legs) 4.0 times that of a normal cow. In order to provide the same relative support,
(a) how much larger would the cross-sectional area of super-cow's legs have to be?
"S" stands for "Super Cow"
"N" stands for "Normal Cow"
Stress on legs is to be the same\(\mathrm {M_S/A_S = M_N/A_N}\) since the weight of the cow is proportional to its mass and A is the cross-section area of the legs.
\(\mathrm {A_S/A_N = M_S/M_N = 4}\)
(b) how much larger would the leg diameter have to be?As shown in part (a)
\(\mathrm {A_S/A_N = 4}\)but \(\mathrm {A_S/A_N = (L_S/L_N)^2}\) where \(\mathrm {L}\) is the linear dimension, in this case, the diameter of the leg.
\(\mathrm {Therefore\;(L_S/L_N)^2 = 4 \\ L_S/L_N = 2}\)



