Study Guide 15 - Turbulent, Bolus and Pulsatile Flows, Aneurysms

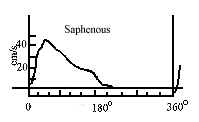
  1. The graph shows the blood flow speed in the saphenous artery of a dog

    The graph shows the blood flow speed in the saphenous artery of a dog with pulse frequency \(\mathrm {2.5 \;s^1.}\) The blood viscosity is \(\mathrm {4 \times 10^3\; N\; s\; m^2 }\)and the thickness of the wall is \(\mathrm {10^3\; m.}\) What is the flow per minute in this vessel? \(\mathrm {Diameter = 1.0 \times 10^3\; m}\)

    Warning: Note that the vertical axis is in \(\mathrm {cm/s.}\) How would you change it to \(\mathrm {cm^3 s^1?}\)
     

    The vertical axis of the graph is a velocity (cm/s). If it is multiplied by an area in cm2 it would be a volume per unit time cm3/s. Clearly the vertical axis must be multiplied by the cross-sectional area of the artery, A.

    Then:

    \(\mathrm {\frac{Vol}{time}= \bigg[\frac{area\; of\; graph}{time} \bigg] A}\)

    The time for one pulse is represented as one cycle of \(\mathrm{360^\circ.}\) If the pulse frequency is \(\mathrm {2.5s^{-1},}\) what is the duration of one pulse?

    The period (time per pulse) is \(\mathrm {1/2.5 = 0.4 \;s}\)

    We will approximate the area of the graph with that of a triangle. What is the altitude of the triangle in cm/s?

    The altitude of the triangle is about \(\mathrm {43 \;cm/s.}\)

    Knowing that the pulse period is 0.4 s, what is the base of the triangle in s?

    The base is about \(\mathrm {(210/360)0.4 = 0.23\; s.}\)
    The area of a triangle is given by:

    \(\mathrm {Area = ½\;base\; X\; height = (½)(0.23s)(43\; cm/s) = 4.95 \;cm}\)

    Now recall the expression for volume/s

    \(\mathrm {\frac{Vol}{time} = \frac{area\;of\; graph}{time}A\\ \frac{Vol}{time} = \bigg[\frac{4.95\; cm}{0.4 \;s}\bigg] \pi (0.05 \; cm)^2 = 0.1\; cm^3 /s}\)
     


     
  2. What is the tension in a capillary wall if the blood pressure is \(\mathrm {30\; mm\; Hg}\) and the radius \(\mathrm {4\; \mu m?}\)
     

    The relation between internal pressure P, wall tension T and radius r for a cylindrical pipe is
    \(\mathrm {P = T/r,}\)   or

    \(\mathrm {T = Pr}\)

    \(\mathrm {P = 30 \;mmHg = \rho gh = 13600(9.8)(30 \times 10^{-3}) = 4.0\times 10^3\; Pa}\)

    \(\mathrm{t = 4.0 \times 10^3 \times 4.0 \times 10^{-6} = 1.6 \times 10^{-2}\; N/m}\)


     
  3. The tension in the wall of an artery of radius \(\mathrm{5.00 \times 10^3 \;m}\) is \(\mathrm {650\; N\; m^1.}\) Further from the heart, a constriction in the same vessel decreases the cross-sectional area to one half of what it was. What is the tension in the wall at this point? Assume flow is steady and that \(\mathrm{v = 0.700\; m\; s^1}\) at the wider portion. Neglect viscosity and assume negligible change in elevation.
     

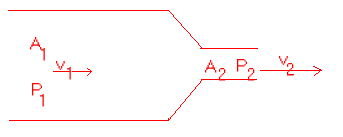
    diagram indicating a constriction in a vessel

    The equation of continuity is: \(\mathrm{Q_1 = Q_2 = A_1v_1 = A_2v_2}\)

    \(\mathrm {A_1v_1 = 0.5A_1v_2 \\ v_2 = 2v_1}\)

    If \(\mathrm {A_2 = ½A_1,}\) then:
    \(\mathrm {r_2 = (½)^½r_1}\)

    This is a problem involving:
    Non-viscous flow and Bernoulli's equation.
    \(\mathrm {P_1 + ½\rho v_1{^2} + \rho gh_1 = P_2 + ½\rho v_2{^2} + \rho gh_2}\)

    Since the level doesn't change, \(\mathrm {h_1 = h_2}\)
    \(\mathrm {P_1 + ½\rho v_1{^2} = P_2 + ½\rho v_2{^2}}\)

    For a cylindrical tube (curved only in one direction) the relation between pressure (P), tension (T), and radius (r) is:

    There is one \(\mathrm {T/r}\) for each curvature so for a cylinder, \(\mathrm {P = T/r}\)

    \(\mathrm {T_1/r_1 + ½\rho v_1{^2} = T_2/r_2 + ½\rho v_2{^2} \\ 650/5 \times 10^{-3} + ½(1000)(0.7)2 = T/(5 \times 10^{-3}/2½) + ½(1000)(2 \times 0.7)^2 \\ T = 457 \;N/m}\)

     


     
  4. An extensible tube was found to stretch to a radius of \(\mathrm {1.0 \times 10^3 \;m}\) when the pressure inside was greater than the outside pressure by \(\mathrm {60\; N\; m^2.}\) A student was given the problem of finding the conditions under which the end of the tube could be placed in a liquid and a hemispherical bubble of radius \(\mathrm {1.0 \times 10^3 \;m}\) be blown into it. The student was surprised to find that it did not matter how far down into the fluid the tube was placed and that it could be done only for a particular value of the surface tension of the fluid. What is the surface tension?
     

    diagram illustrating excess pressure in a tube

    Excess pressure inside the tube must be \(\mathrm {60\;Pa}\) to keep the radius of the tube at \(\mathrm {1.0 \times 10^{-3}\; m.}\) Therefore the pressure inside must be \(\mathrm {60\; +\rho gh.}\)

    To blow a bubble under a liquid surface the \(\mathrm {Excess\; pressure = 2\gamma/R}\)
    Therefore the pressure inside is \(\mathrm {2\gamma/R + \rho gh}\)

    But we previously saw that the pressure inside was \(\mathrm {60\; +\rho gh}\)

    Therefore \(\mathrm {2\gamma /R = 60,}\) independent of h and,
    \(\mathrm {\gamma = (60/2)R = (60/2)(1.0\times 10^{-3}) = 0.030\; N/m}\)


     
  5. Draw graphs of tension (in \(\mathrm {N\; m^1}\)) versus radius for

    (a) a soap bubble.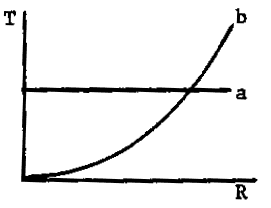

    diagram of tension on a soap bubble

    The tension in a soap bubble is the surface tension \(\gamma,\) which is a property of the fluid and is independent of R. Thus the curve (a) is a horizontal line.

    A blood vessel is an elastic membrane in which the tension increases non-linearly with R. This is shown in curve (b) and also in Fig 10.13 in the text.



    (b) a cylindrical blood vessel.

     diagram of tension on a soap bubble

    The tension in a soap bubble is the surface tension \(\gamma,\) which is a property of the fluid and is independent of R. Thus the curve (a) is a horizontal line.

    A blood vessel is an elastic membrane in which the tension increases non-linearly with R. This is shown in curve (b) and also in Fig 10.13 in the text.