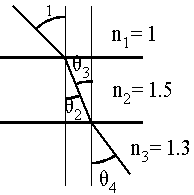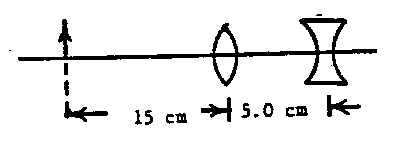Study Guide 3 - Optics of the Eye
Note: If you wish further help on Snell's Law, you may find this bending light video entertaining and useful.
The figures below correspond to questions 1-3.
- One of the diagrams below is correct. Which one, A, B, C or D?
Recall that a light ray bends towards the normal when it passes from a low index of refraction (\(\mathrm {n_1 = 1.0}\), in this case) medium to a higher index of refraction \(\mathrm {(n_2 = 1.5)}\) medium. In the figure, only the rays in (b) and (d) bend towards the normal at the upper interface.
At the lower interface, the light ray is passing from a higher index of refraction \(\mathrm {(n_2 = 1.5)}\) medium to a lower index of refraction \(\mathrm {(n_3 = 1.3)}\) material. In this case, the light ray should bend away from the normal at the lower interface. In (b), the light ray bends away from the normal, whereas the light ray in (d) bends towards the normal.
Therefore, the drawing in (b) is the correct drawing.
- For the correct situation in Q1 above, calculate
\(\mathrm {\theta_2, \; \theta_3, \; \theta_4 \; if\; \theta_1 = 30^\circ.}\)
B is the correct situation from Q1
Which is the correct equation to use in this case relating: \(\mathrm {\theta_1, \; \theta_2, \; n_1, \;n_2?}\)
\(\mathrm {n_1 \; \sin \; \theta_1 = n_2 \; \sin \; \theta_2}\)
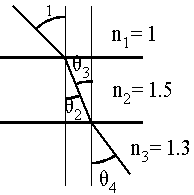
\(\mathrm {In\; this \;case\; n_1 = 1.0, \;n_2 = 1.5, \; \theta_1 = 30^\circ.}\)
\(\mathrm {1\; \sin\; 30 = 1.5\; \sin\; \theta_2}\)
\(\mathrm {\theta_2 = 0.5/1.5 = 0.333}\)
\(\mathrm {\theta_2 = 19.5^\circ.}\)This is also the value of \(\mathrm{\theta_3}\)
Now evaluating \(\mathrm {\theta_4}\)
\(\mathrm {n_2 \sin \; \theta_3 = n_3 \sin\; \theta_4}\)
\(\mathrm {1.5\; \sin\; 19.5 = 1.3\; \sin \; \theta_4}\)
\(\mathrm {\sin\; \theta_4 = (1.5)(0.333)/(1.3) = 0.385}\)
\(\mathrm{\theta_4 = 22.6^\circ}\)
- What is the critical angle for an interface of glass (n = 1.50) in water (n = 1.33)?
What is the angle of refraction at the critical angle?
The situation is shown below.
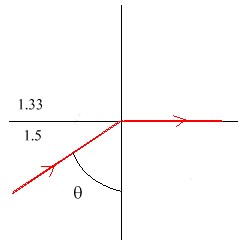
Use Snell's Law
\(\mathrm {1.5\; \sin\; \theta = 1.33\; \sin\; 90}\)
\(\mathrm{\sin\; \theta = 0.887}\)
\(\mathrm {\theta = 62.5^\circ}\) - Are p, q, R positive or negative in the following?
p - POSITIVE The object is measured upstream from the vertex.
q - POSITIVE Image distances are measured positive downstream from the vertex.
R - POSITIVE Radii are measured positive pointing upstream.
p - POSITIVE The object is measured upstream from the vertex.
q - NEGATIVE Image distances are measured positive downstream from the vertex.
R - POSITIVE Radii are measured positive pointing upstream.
p - POSITIVE The object is measured upstream from the vertex.
q - POSITIVE Image distances are measured positive downstream from the vertex.
R - NEGATIVE Radii are measured positive pointing upstream.
- A paperweight consists of a cylinder of glass (n = 1.5) 1.00 cm high and of radius 2.00 cm on which is mounted a hemisphere of radius 2.00 cm. The weight is placed on a sheet of paper so that an inkspot is at the centre of its plane surface C. Looking from above, how far below the upper surface of the glass will the spot appear to be?
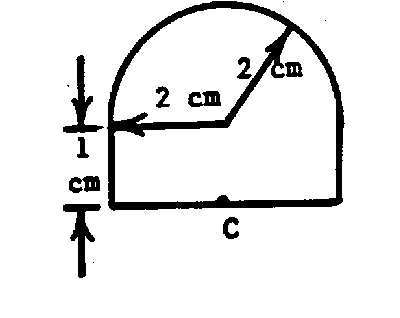
Hint: Draw a light ray originating at C and stick rigorously to the sign convention.
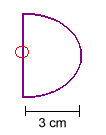
Light is travelling towards the right.
\(\mathrm {n_1/p + n_2/q = (n_2 - n_1)/R}\)The index in the object space is 1.5 in this case.
The index in the image space is 1 in this case.\(\mathrm {1.5/3 + 1/q = (1 - 1.5)/(-2)}\)
\(\mathrm {q = -4\; cm}\)
A negative value for q means that the distance from the curved surface of the paperweight to the image is against the flow of light. That is, the image is 4 cm to the left of the curved surface of the paperweight.
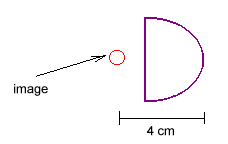
- Are p, q and f positive or negative in the following?
(a)
p - POSITIVE Object distances are measured positive upstream.
q - POSITIVE Object distances are measured positive upstream.
f - POSITIVE Converging lenses have f positive.
(b)
p - POSITIVE Object distances are measured positive upstream.
q - POSITIVE Converging lenses have f positive.
f - NEGATIVE Diverging lenses have f negative.
(c)
p - POSITIVE Object distances are measured positive upstream.
q - NEGATIVE Image distances are measured positive downstream.
f - POSITIVE Converging lenses have f positive.
- In the drawings in Q6 take the case:
(a) p = 20.0 cm, f = 12.0 cm
(b) p = 20.0 cm, f = -12.0 cm
(c) p = 10.0 cm, f = 12.0 cm
In each case find q and the magnification.
(a)
\(\mathrm {p = 20.0 \;cm, f = 12.0 \;cm}\)
\(\mathrm {1/p + 1/q = 1/f}\)
\(\mathrm {1/20 + 1/q = 1/12}\)
\(\mathrm {1/q = 1/12 - 1/20 = (20 - 12)/(12\times20) = 8/240}\)
\(\mathrm {q = 240/8 = 30.0\; cm}\)
Now find the magnification:
\(\mathrm {m = -q/p = -30/20 = -1.5}\)
i.e., Image is magnified and inverted as in the figure.
(b)
\(\mathrm {p = 20.0 \;cm, f = -12.0 \;cm}\)
\(\mathrm {1/p + 1/q = 1/f}\)
\(\mathrm {1/20 + 1/q = 1/-12}\)
\(\mathrm {1/q = -1/12 - 1/20 = -32/240}\)
\(\mathrm {q = -240/32 = -7.5 \;cm.}\) (Image is upstream and virtual)
Now find the magnification:
\(\mathrm {m = -q/p = -(-7.5)/20 = 0.375}\)
i.e., Image is demagnified and erect as in the figure.
(c)
\(\mathrm {p = 10.0 \;cm, f = 12.0 \;cm}\)
\(\mathrm {1/p + 1/q = 1/f}\)
\(\mathrm {1/10 + 1/q = 1/12}\)
\(\mathrm {1/q = 1/12 - 1/10 = -2/120}\)
\(\mathrm {q = -120/2 = -60 \;cm.}\)
Image is upstream and virtual. (Object is inside the focal length and the lens is operating as a simple magnifying glass)
Now find the magnification:
\(\mathrm {m = -q/p = -(-60)/10 = 6}\)
i.e., Image is magnified and erect. 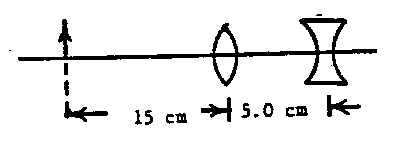
Two lenses of focal length 10.0 and -10.0 cm respectively are separated by 5.00 cm. An object 1.00 cm high is placed 15.0 cm to the left of the converging lens.
(a) Where, and what size is the final image? Is the image erect or inverted, real or virtual?
(b) Is the object distance for the 2nd lens positive or negative?(a) We must first solve for the 1st lens.
\(\mathrm {1/p + 1/q = 1/f}\)
\(\mathrm {1/15 + 1/q = 1/10}\)
\(\mathrm {1/q = 1/10 - 1/15 = 5/150}\)
\(\mathrm {q = 150/5 = 30 \;cm.}\)
The image formed by the 1st lens is 30 cm downstream (to right) from the lens.
Therefore it is 25 cm downstream from the 2nd lens.
The image formed by the first lens becomes the object for the second lens.
(b) NEGATIVE
For the 2nd lens:
\(\mathrm {p = -25 \;cm, f = -10 \;cm}\)\(\mathrm {1/p + 1/q = 1/f}\)
\(\mathrm {1/-25 + 1/q = 1/-10}\)
\(\mathrm {1/q = -1/10 + 1/25 = (10 - 25)/250 = -15/250}\)
\(\mathrm {q = -250/15 = -16.7 \;cm}\)Therefore the final image is 16.7 cm to the left (upstream) of the 2nd lens or 16.7 - 5 = 11.7 cm to the left of the 1st lens.
Now find the magnification
For 1st lens: \(\mathrm {p_1 = 15 \;cm, \;q_1 = 30 \;cm}\)
For 2nd lens: \(\mathrm {p_2 = -25 \;cm, \;q_2 = -16.7 \;cm}\)
\(\mathrm {m_1 = -q_1/p_1 = -30/15 = -2}\)
\(\mathrm {m_2 = -q_2/p_2 = -(-16.7)/(-25) = -0.668}\)
\(\mathrm{m = m_1m = (-2)(-0.668) = 1.34}\)\(\mathrm {Image \;size = m(Object\; Size) = 1.34\times1 = 1.34 \;cm}\)
Image is magnified and virtual
This is, in fact, the optical arrangement of the Galilean telescope used in opera glasses.