Study Guide 7 - Ionizing Radiation

Rewrite this equation with the atomic mass number and the atomic number (nuclear charge) explicit for each item in the equation:

\(\mathrm {? =\;\begin {smallmatrix}^{12} \\ _6 \end{smallmatrix} \;C\; +\; \begin {smallmatrix} ^0 \\ _{-1} \end{smallmatrix}e + v }\)

The equation must balance so that the total atomic mass number and the total atomic number is the same on each side.
\(12 + 0 + 0 = 12 \\ 6 - 1 + 0 = 5\)

Equation is:

\(\mathrm {\begin {smallmatrix} ^{12} \\ _5 \end{smallmatrix} ? =\;\begin {smallmatrix}^{12} \\ _6 \end{smallmatrix} \;C\; +\; \begin {smallmatrix} ^0 \\ _{-1} \end{smallmatrix}e + v }\)

Go to the Periodic Table to determine the unknown.

\(224 = 220 + 4 \\ 88 = 86 + 2\)

\(\mathrm {\begin{smallmatrix} 224 \\ 88 \end{smallmatrix} Ra = \begin {smallmatrix} 220 \\ 86 \end {smallmatrix} ? +\; _2^4 \alpha}\)

Go to the Periodic Table to identify the unknown.

\(210 = 210 + 0 \\ 83 = 84 - 1\)

\(\mathrm {\begin{smallmatrix} 210 \\ 83 \end{smallmatrix} \; Bi = \begin{smallmatrix} 210 \\ 84 \end{smallmatrix} \; Po\; + \begin{smallmatrix}0 \\ -1 \end{smallmatrix}\;?}\)

What is this particle?

\(\mathrm {\begin{smallmatrix} 210 \\ 83 \end{smallmatrix} \; Bi = \begin{smallmatrix} 210 \\ 84 \end{smallmatrix} \; Po\; + \begin{smallmatrix}0 \\ -1 \end{smallmatrix}\;e}\)

The unknown is an electron or \(\beta \) particle.

The relation between half life and decay constant is:

\(\mathrm {\lambda = 0.693/T_½}\)

\(\mathrm {For\; T_½ = 15 \; day,\; \lambda = 0.693/15 = 0.0462 \;day^{-1}}\)

\(\mathrm {0.0462 \; day-1(1/24 \times 3600) day/s = 5.35 \times 10^{-7} s^{-1}}\)

\(\mathrm {\lambda _e = \lambda_p + \lambda_b = 0.080 + 0.050 = 0.130\; day^{-1}}\)

 \(\mathrm {T_½ = 0.693/\lambda_e = 0.693/0.130 = 5.3 \;days}\)

\(\mathrm {Since\; _ ½T_p \;is \;very \;long \;then \; \lambda_p = 0}\)

\(\mathrm {Therefore\; \lambda_e = \lambda_b = \lambda}\)

 \(\mathrm {Also\; \lambda (A) = 1.5 \lambda (D)}\)

For Aristophanes:
\(\mathrm {NA = 2N_0{e^{-\lambda (A) t}} = 2N_0e ^{-1.5\lambda(D)t}}\)

For Demetrius:
\(\mathrm {N_D = N_0 = N_0e ^{-\lambda(D)t}}\)

When \(\mathrm {N_A = N_D}\)
\(\mathrm {2N_0e^{-1.5l\lambda (D)t} = N_0e^{-\lambda(D)t}}\)

Taking natural logarithms:
\(\mathrm {ln \;2 - 1.5 \lambda (D) t = -\lambda (D) t}\)

\(\mathrm {0.5 \lambda (D) t = ln \;2 \\ t = ln\; 2/(0.5)(0.10) = 14\; days}\)

\(\mathrm {C ~ 1/d^2 \\ C_1/C_2 = (d_2/d_1)^2 \\ d_2\;^2 = (900/600)(300)^2 \\ d_2 = (9/6)^½ 300 = 370 \;cm}\)
 

\(\mathrm {I = I_0e^{-\mu_m \rho x }}\)

Copper: \(\mathrm {\rho x = 9 \times 5 = 45}\)
Zircon: \(\mathrm {\rho x = 4.7 \times 9 = 42.3}\)
Since \(\mathrm {\mu_ m}\) is the same in each case then if \(\mathrm {\rho x = 45}\) just absorbs all the \(\gamma\) s then \(\mathrm {\rho x = 42.3}\) will be insufficient.

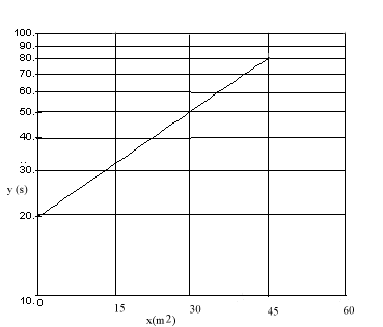
This is a semi-log plot so

\(\mathrm {y = c \;e^{kx} \\ \ell n \;y = \ell n \;c + kx}\)

Therefore a semi-log plot gives a straight line.
In the graph c is the intercept so c = 20 s.
The slope of the graph is k. Using the points (45,80) and (0,20)

\(\mathrm {k = \frac{\ell n80 - \ell n20}{45 - 0}= \frac{\ell n (80/20)}{45}= \frac{1.386}{45}= 0.031}\)

Find the units of k:

The quantity kx must be dimensionless (since it appears as an exponent).
Since x has units m² then k must have units m^-2
\(\mathrm {k = 0.031 \;m^{-2}}\)

Equivalent Dose (gray) = QF X Dose (sievert)
Dose = 1.0/1.01 = 0.91 gray

\(\mathrm {Energy = 0.91 (gray) \times 1.00 (J/kg) \times 10\times 10^{-3} (kg) \\ = 9.09\times 10^{-3} \;J}\)

Alpha particles have a high LET (linear energy transfer) so would be entirely stopped by the skin where they might do much damage. They would not reach the teeth.