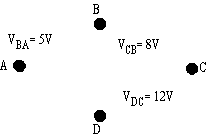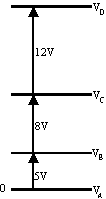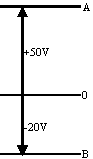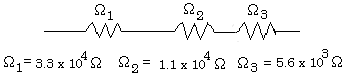Study Guide 8 - Electricity

  1. If you could somehow isolate at a single point, one gram mole of Na+ ions, what total charge would you have at the point? Recall: Avogadro's number \(\mathrm {N_A = 6.02\times10^{23}(g\; mol)^{-1}}\)
     

    \(\mathrm {Q = Nq = 6.02\times 10^{23} \times 1.6 \times 10^{-19} = 9.6 \times 10^4 \;C}\)


     
  2. (a) A \(\mathrm {Na^+ \;ion}\) is placed one-quarter of the distance between two \(\mathrm {Ca^{++} \; ions}\) which are 10.0 nm apart. Find the resultant force on the \(\mathrm {Na^+\; ion}\) assuming that the solvent is water \(\mathrm {(\kappa = 80.4).}\) (You should be able to answer the question using either Coulomb's Law or the Field method)
     

    Coulomb's Law

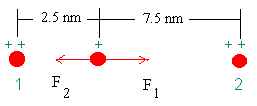
    diagram of Colulomb's Law

    The force \(\mathrm {F_1}\) is that due to the left-hand \(\mathrm {Ca^{++}}\) and the \(\mathrm {Na^+.}\) It acts in the \(\mathrm {+x}\) direction. \(\mathrm {F_2}\) is that due to the right-hand \(\mathrm {Ca^{++};}\) it acts in the \(\mathrm {-x}\) direction.

    \(\mathrm {F_1 = \frac{k(2e)e}{\kappa(2.5\times 10^{-9})^2}= \frac{9 \times 10^9 (2)(1.6 \times 10^{-19})^2}{80.4(2.5 \times 10^{-9})^2} = 9.17 \times 10^{-13}N}\)

    \(\mathrm {F_2 = \frac{k(2e)e}{\kappa(7.5\times 10^{-9})^2}= \frac{9 \times 10^9 (2)(1.6 \times 10^{-19})^2}{80.4(7.5 \times 10^{-9})^2} = 1.02 \times 10^{-13}N}\)

    \(\mathrm {F = F_1 - F_2 = (9.17 - 1.02)\times 10^{-13} \ N}\)


    Field Method
     

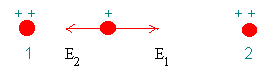
    diagram of Field Method

    \(\mathrm {E_1 = \frac{k(2e)}{\kappa(2.5 \times 10^{-9})^2}= \frac{9 \times 10^9 (2)(1.6 \times 10^{-19})}{80.4 (2.5 \times 10^{-9})^2}= 5.731 \times 10^6 \; N/C}\)

    \(\mathrm {E_2 = \frac{k(2e)}{\kappa(7.5 \times 10^{-9})^2}= \frac{9 \times 10^9 (2)(1.6 \times 10^{-19})}{80.4 (7.5 \times 10^{-9})^2}= 0.637 \times 10^6 \; N/C}\)

    \(\mathrm {E = E_1 - E_2 = (5.731 - 0.637)\times 10^6\; N/C}\)


    What is the relation between field and force?

    \(\mathrm {F = qE = (1.6\times 10^{-19})(5.1\times 10^6 =8.2\times 10^{-13}\; N \;as \;before.}\)



    (b) Where would the resultant force on the \(\mathrm {Na^+\; ion}\) be zero? (There are two answers to this part.)
     

    The force is zero at: (more than 1 correct answer)

    Infinity - Since \(\mathrm {F \sim 1/r^2}\) then this is one of the places where the force is zero.

    Half way between the \(\mathrm {Ca^{++} \; ions}\) - At this location the two forces (or fields) would be equal and opposite.


     
  3. A \(\mathrm {Cl^- \; ion}\) is in a field of \(\mathrm {100\; NC^{-1}.}\) Calculate the ratio of the Coulomb force to the weight of the ion. (The weight is the gravitational force on the ion at the surface of the Earth.) Recall \(\mathrm {w = mg}\) and \(\mathrm {g = 9.8\; N/kg}\) on the Earth's surface. Assume a chlorine mass number 35. The value of Avogadro's number is \(\mathrm {6.02\times 10^{23} (g \;mol)^{-1}}\)
     

    First find the electrical force.
    As before \(\mathrm {F = qE = 1.6\times 10^{-19} \times 100 = 1.6 \times 10^{-17} \; N}\)

    We must find the mass of the Cl ion. We know that Avogadro's number of atoms has a mass of 35 gm or 0.035 kg.
    Therefore the mass of one \(\mathrm {Cl \;atom = 0.035/6.02 \times 10^{23} = 5.8 \times 10^{-26} kg.}\)
    \(\mathrm {Weight = mg = 5.8\times 10^{-26} \times 9.8 = 5.7 \times 10^{-25} \; N}\)
    \(\mathrm {Ratio = F_e/F_g = 1.6\times 10^{-17}/5.7 \times 10^{-25} = 2.8 \times 10^7}\)

    Electrical forces are much stronger than gravitational forces. We are usually not aware of them because normal matter is electrically neutral.


     
  4. Potential differences between some pairs of points are given below. Calculate the unknown potential differences \(\mathrm {V_{CA}, V_{AD}, V_{DB}.}\)

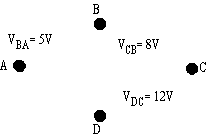
    Potential differences between pairs of points

    Hint: When considering potential differences one may arbitrarily assign any point a potential of zero (rather than "zero at infinity"). E.g., if you set \(\mathrm {V_A = 0,}\) then \(\mathrm {V_B}\) must be \(\mathrm {+5\; V}\) \(\mathrm {(since\; V_{BA} = 5 \;V);}\) continue for values of \(\mathrm {V}\) at \(\mathrm {C}\) and \(\mathrm {D}\) and then determine \(\mathrm {V_{CA}}\) etc.
     

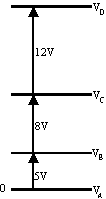
    diagram of voltage ladder

    If we arbitrarily set \(\mathrm {V_A}\) at 0 and then find \(\mathrm {V_B, V_C, V_D,}\) we could represent them as a "voltage ladder". From the ladder it is easy to see:
    \(\mathrm {V_{CA} = 8 + 5 = 13 \;V \\ V_{DA} = 12 + 8 + 5 = 25 \;V \\ Therefore\; V_{AD} = -25 \;V \\ V_{DB} = 12 + 8 = 20\; V}\)


     
  5. At a point A near some ions in solution, the potential is \(\mathrm {50 \;V}\), i.e., \(\mathrm {V_A = 50 \;V}\) relative to 0 at infinity.

    (a) What "electrical work" (i.e., work against the E-field of the ions must you do to move a \(\mathrm {SO^=4}\) at constant speed (no KE change) from infinity to point A?
     

    \(\mathrm{W = qV = -2(1.6\times 10^{-19})(50) = -1.6\times 10^{-17} \; J}\)

    In other words, you would not have to do work (i.e., pushing the \(\mathrm {SO^=4}\)) but it would do work on you (i.e., pull you). Remember a negative charge runs up a potential hill.



    (b) What "electrical work" would you have to do to move the \(\mathrm {SO^=\;_4}\) back from \(\mathrm {A}\) to infinity?
     

    Now you would have to do work equal to that done on you in part (a). The amount of work done is equal to the amount in part (a) but positive i.e., \(\mathrm {1.6\times 10^{-17} \; J.}\)



    (c) What is the electrical \(\mathrm {PE}\) of the \(\mathrm {SO^=\;_4}\) ion at the point \(\mathrm {A}\)?
     

    Potential energy is equal to the work done in putting the charge in position, i.e., the answer is given by the answer to part (a).



    (d) What work would the electric field do on the \(\mathrm {SO^=\;_4 \; ion}\) if it moves from \(\mathrm {A}\) to infinity?
     

    Since you would have to do work to push the ion to infinity, then the work done by the field is negative. In other words the answer is the same as in part (a), i.e. \(\mathrm {-1.6\times 10^{-17} \;J.}\)


     
  6. Referring to Question 5. At a second point \(\mathrm {B,}\) the potential is \(\mathrm {V_B = -20 \;V.}\)

    (a) What electrical work must you do to move the ion at constant speed from \(\mathrm {A}\) to \(\mathrm {B}\)?
     

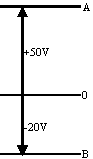
    Diagram indicating work to be done to move an ion from A to B

    \(\mathrm {V_{BA} = - 20 - 50 = -70 V \\ W = qV = -2(1.6 \times 10^{-19})(-70) = 2.24 \times 10^{-17} \; J}\)


    (b) What is the change in the \(\mathrm {SO^=\;_4}\) ion's electrical \(\mathrm{PE}\) when it goes from \(\mathrm {A}\) to \(\mathrm {B}\)?
     

    Potential energy is equal to the work done in putting the charge in position, i.e., the answer is given by the answer to part (a).


     
  7. In 2.0 seconds, \(\mathrm {10^{12} H^+ \; ions}\) flow through a capillary tube 1.0 mm in diameter. Calculate the current and the current density.
     

    The definition of current is Charge/time

    \(\mathrm {I = Q/t = (10^{-12})(1.6\times 10^{-19})/2 = 8 \times 10^{-8}\; A}\)

    \(\mathrm {Current \;density: J = I/Area \\ J = 8 \times 10^{-8}/\pi (0.5 \times 10^{-3})^2 = 0.2 \;A/m^2}\)


     
  8. A current of \(\mathrm {10.0 \;mA}\) flowing through (along) your finger is painful. Suppose the current is carried by singly ionized atoms. How many ions per second are flowing? \(\mathrm {(1 \; mA = 10^{-3} \; A)}\)
     

    \(\mathrm {I = qN/t = (1.6 \times 10^{-19})N/1 = 1.0 \times 10^{-3} \\ N = 6.25 \times 10^{16} \;ions/s}\)


     
  9. Currents and current paths are shown in the diagram below. What are the currents and their directions in paths \(\mathrm {A}\) and \(\mathrm {B}\)?

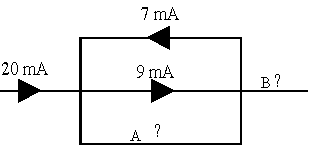
    Diagram of currents and directions in paths A and B
     

    Path B

    The current must be preserved. Therefore there must be \(\mathrm{20\; mA}\) always flowing to the right. From this it follows that the current in \(\mathrm {B}\) is \(\mathrm {20\; mA.}\)

    Path A

    There is a net current of \(\mathrm {9 - 7 = 2 \;mA}\) flowing to the right, so the branch \(\mathrm {A}\) must have \(\mathrm {20 - 2 = 18 \;mA}\) flowing to the right.


     
  10. Axoplasm has a resistivity of \(\mathrm {25\; \Omega \; cm.}\) This fluid is drawn up into a microelectrode of 0.100 mm diameter and 0.700 cm long. What is the resistance of this column of fluid?
     

    \(\mathrm {R = \rho A/l = 25(\Omega\; cm)\pi(0.005 )^2(cm^2)/0.7 \;cm. \\ = 2.2 \times 10^5\; \Omega.}\)


     
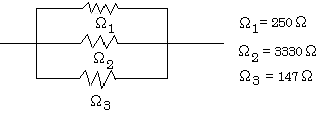
  11. Diagram of resistors

    (a) What single resistance would be equivalent to the three shown above?
     

    The three resistors are in parallel. What is the rule for resistors in parallel?

    \(\mathrm {1/R = 1/R_1 + 1/R_2 + 1/R_3 \\ 1/R = 1/250 + 1/3330 + 1/147  \Rightarrow R = 90.0 \; \Omega}\)



    (b) What total current would flow through the network if a potential difference of 10 V were applied across it?
     

    What is the relation between V, I and R?

    \(\mathrm {V = IR \;and \; from \; part \; (a)\; R = 90.0 \; \Omega \\ I = 10 / 90.0\; \Omega = 0.111 \;A}\)



    (c) What current would flow through each of the three resistors?
     

    The \(\mathrm {10 \; V}\) is applied across each of the resistors.
    \(\mathrm {For\; R_1: I_1 = V / R_1 = 10 / 250 = 0.04 \;A}\)

    \(\mathrm {For\; R_2: I_2 = V / R_2 = 10 / 3330 = 0.0030 \;A}\)

    There are 2 ways to determine the third and last current:

    • \(\mathrm {As\; before\; For\; R_3: I_3 = V / R_3 = 10 / 147 = 0.068 \; A \\ Notice, \;as \;required: 0.04 + 0.0030 + 0.068 = 0.111\; A}\)
       
    • \(\mathrm {Knowing\; that\; the\; total\; current\; must\; be\; 0.111 \;A \; then \\ I_3 = 0.111 - I_1 - I_2 = 0.111 - 0.04 - 0.0030 = 0.068\; A \;as\; in\; 1.}\)

     
  12. What single value of resistance would be equivalent to the three shown below?

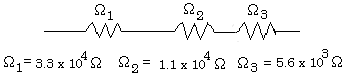
    Diagram indicating 3 resistors, \Omega_1 = 3.3 \times 10^4 \Omega, \Omega_2 = 1.1 \times 10^4 \Omega, |Oemga_3 = 5.6 \times 10^3 \Omega
     

    The three resistors are in series. What is the rule for resistors in series?

    \(\mathrm {R = R_1 + R_2 + R_3 \\ R = 3.3 \times 10^4 + 1.1 \times 10^4 + 5.6 \times 10^3} \)

    \(\mathrm {R = 5.0 \times 10^4 \; \Omega}\)


     
  13. For the series-parallel arrangement of resistors find: \(\mathrm {V_{AB}, V_{BC}, V_{AC}}\) and the \(\mathrm {current}\) through each of the parallel paths.
     

    \(\mathrm {V_{AB}}\)
    What is the relation between V, I and R?

    \(\mathrm {V = IR, Therefore\; V_{AB} = I_{AB}R_{AB} \\ V = (1.00 \times 10^{-3} \;A ) ( 8300\; \Omega ) =  8.33 \;V}\)


    \(\mathrm {V_{BC}}\)
    We must find the equivalent resistance of the parallel part of the circuit. What is the relationship for resistors in parallel?

    \(\mathrm{1/R = 1/R_1 + 1/R_2 \\ 1/R = 1/2500 + 1/1.0 \times 10^4   \Rightarrow R = 2000\; \Omega}\)

    The voltage across this resistor is:
    \(\mathrm {V_{BC} = I_{BC}R_{BC} = 1.0 \times 10^{-3} \times 2000 = 2.0 \; V}\)


    \(\mathrm {V_{AC}}\)
    \(\mathrm {V_{AC} = V_{AB} + V_{BC} = 8.33 + 2.00 = 10.33\;V}\)


    \(\mathrm{Current}\)

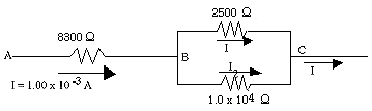
    series-parallel arrangement

    \(\mathrm{Since V_{BC} = 2.0\; V \\ Then\; I_1 = V / R_1 = 2.0 / 2500 = 8.0 \times 10^{-4} \;A \\ and\; I_2 = V / R_2 = 2.0 / 1.0 \times 10^4 = 2.0 \times 10^{-4} \;A \\ Notice\; I = I_1 + I_2 = 8.0 \times 10^{-4} + 2.0 \times 10^{-4} = 1.0 \times 10^{-3} \;A\; as\; it\; should.}\)